Trying to understand vector conversion matrices

[FrankJ777]

Homework Statement

This isn't exactly a "problem" per se , but I need to understand it for a course I'm taking. I'm trying to understand the significance and when to use the vector conversion matrices, or just the identities. I'll use an example that I made up, using rectangular to polar coordinates for simplicity so you can see what I'm not understanding.

Homework Equations

I'm fairly comfortable with the following identities to convert polar to rectangular and vice verse :
x = ρ cos Φ
y = ρ sin Φ
ρ = √(x² + y²)
Φ = tan^-1 x/y

but I've difficulty with:

A_x = A_ρ cos Φ - A_Φ sinΦ
A_y = A_ρ sin Φ + A_Φ cosΦ

A_ρ = A_x cos Φ + A_y sinΦ
A_Φ = -A_x sin Φ + A_y cosΦ

In this example: (the lowercase scripts indicate unit vectors.)
A_polar = 10 a_ρ + π/3 a_Φ or

The Attempt at a Solution

Using:
x = ρ cos Φ, y = ρ sin Φ
with ρ=10, Φ = π/3
⇒ A_rect = 5 a_x + 5√3 a_y

which seems correct
but using the matrix and pluging in for A_ρ andA_Φ

A_x = A_ρ cos Φ - A_Φ sinΦ
A_y = A_ρ sin Φ + A_Φ cosΦ
i get:
A_x = 10 cos π/3 - π/3 sin π/3 = 5 - π√3 / 6 ≈ 4
A_y = 10 sin π/3 + π/3 cos π/3 = 5√3 + π/6 ≈ 9.18

So I end up with a vector A_rect with components :
A_rect = 4 a_x + 9.18 a_y

So why don't both methods agree.

 

[Lucas SV]

You are confusing coordinates with vector components. This is natural. In early maths education we are so used to the idea that vectors are arrows from the origin to a point, since this is what we have been taught. This is all good as long as we use cartesian coordinates in euclidean space. As soon we start studying non-euclidean spaces, or even curvilinear coordinates in euclidean space, we need to adapt. We start attaching vectors to every point.

Polar coordinates are an example of this. At every point in the cartesian plane, attach two unit basis vectors. One is along the radial direction, while the other is along the angular direction. If you do that for every point (except for the origin) you get two vector fields, the radial vector field and the angular vector field. You can do something similar with cartesian coordinates, you can attach an $x$ and $y$ basis vector to each point in the cartesian plane. In the cartesian case this is a bit of an overkill, so we don't find it necessary and we discard the idea completaly. However it becomes indispessible for curvilinear coordinates.

Then you take a vector $A$ at a point $(x,y)$. Since often we want to define $A$ for many points, we can do so by making $A$ a vector field. Anyway, at point $(x,y)$, suppose we defined $A$ with respect to the cartesian basis. Now do a change of basis (at that point), to the radial and angular unit vectors I described. So you find new components for $A$. The change of basis is described by a matrix. This matrix depends on the point you have fixed.

If the point is $(x,y)$, with $x=\rho\cos\Phi$ and $y=\rho\sin\Phi$ (in polar coordinates), at that point, we have the linear transformation of components of $A$ from the polar basis to the cartesian basis, which you already described as
$$\begin{align}
&A_x=A_\rho\cos\Phi-A_\phi\sin\Phi\\
&A_y=A_\rho\sin\Phi+A_\rho\cos\Phi
\end{align}$$
So the key to understanding here is to make a distinction between a change of coordinates and a change of basis at each point. The terminology for all possible vectors attached to a point is called the tangent space at the point. A change of coordinates will induce a change of basis in all the tangent spaces. In particular for curvilinear coordinates, the basis vectors will depend on which tangent space you wish to talk about.

 

[FrankJ777]

a

 

[Lucas SV]

Ok. So I guess I dont' understand what the "new" vector represents. I think I understand that using the unit transformation:
aρ = cos Φ ax + sinΦ ay
aΦ = - sin Φ ax + cosΦ ay
I would get unit vectors, which i think are the basis vectors, which point in the direction of positive change. But I am not sure what the new vector means when applying the vector component transformation.

Technically it is the same vector, written in a different basis (passive view). It doesn't mean much except to say you have rotated the basis at the tangent space. It is however very useful to make this transformation in certain situations.

For example, the vector field $A$ may have angular symmetry (This is common in physical systems), that is it looks the same in every point of a circle centred at the origin. Then one of the components of $A$ does not change, which may simplify calculations considerably, particularly if you need to differentiate $A$. If you did the same calculutations in the cartesian basis, it would be harder.

 

[FrankJ777]

Ok. So I guess I dont' understand what the "new" vector represents. I think I understand that using the unit transformation:
aρ = cos Φ ax + sinΦ ay
aΦ = - sin Φ ax + cosΦ ay
I would get unit vectors, which i think are the basis vectors, which point in the direction of positive change. But I am not sure what the new vector means when applying the vector component transformation.

So in this example what does it mean that:
Ax = 10 cos π/3 - π/3 sin π/3 = 5 - π√3 / 6 ≈ 4.1
Ay = 10 sin π/3 + π/3 cos π/3 = 5√3 + π/6 ≈ 9.18

Ax ≈ 4.1 , Ay ≈9.18
So the new vector A_rect Ax ax + Ay ay⇒ A_rect= 4.1 ax + 9.18 ay

What does it represent??
And when do I apply this transformation?

Thanks. I should have learned this years ago, but I think we just glossed over it.
Bye the way. I'm looking for examples on this, but mostly finding info on rotating the Cartesian plane, for which the vector transformation makes sense for me, as it describes the same vector in relation to the new rotated plane. I'm using rect - polar transformation because its simple, and i think if I understand it then I can apply it to spherical, cylindrical. etc

 

[Lucas SV]

First I will correct my typo.
\begin{align}
&A_x=A_\rho\cos\Phi-A_\Phi\sin\Phi\\
&A_y=A_\rho\sin\Phi+A_\Phi\cos\Phi
\end{align}
I think that now I understand what you were thinking. Let me point out the equations I just wrote apply for an arbitrary vector field $A$. What you have been doing is choosing a specific $A$ because it 'looks' like the right one.

So in this example what does it mean that:
Ax = 10 cos π/3 - π/3 sin π/3 = 5 - π√3 / 6 ≈ 4.1
Ay = 10 sin π/3 + π/3 cos π/3 = 5√3 + π/6 ≈ 9.18

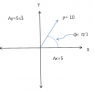
By writting these equations you are assuming you know what $A$ is, i.e. you have just chosen a specific $A$. You have chosen an $A$ in which $A_\rho=10$ and $A_\Phi=\pi/3$, because you wanted to make $A$ look like the point where $A$ is evaluated at (remember however that $A$ is a vector field, so it looks different in different points). Even if you fix the point to be $\rho=10$ and $\Phi=\pi/3$ (from now on we will call this point $p$), $A$ can still be arbitrary.

Now there is nothing wrong with choosing a specific vector field $A$. Suppose we do insist that $A_\rho=10$ and $A_\Phi=\pi/3$ (at the point $p$). Then the picture you drew for $A$ is simply wrong. You should draw $A$ as a vector which starts at the point $p$ and whose projection along the radial basis is 10 and whose projection along the angular basis is $\pi/3$. Another way to think about this is: think of $p$ as the new origin. Then think of two axis, the radial axis is the line which intersects the actual old origin $0$ and the new origin $p$. The angular axis is the line which is perpendicular to the radial axis, and intersects the radial axis at $p$. Then, in this new coordinate system attached to $p$, $A$ will be represented as the vector $(10,\pi/3)$, so walk $10$ steps from $p$ along the radial axis (in which direction? there are two. Pick the direction that increases your radial coordinate in the usual old system), then walk $\pi/3$ steps along a line parallel to the angular axis (in which direction? there are two. Pick the direction that increases your angular coordinate in the usual old system). I hope you can draw this.

Once you have this picture, the calculation for $A_x$ and $A_y$ simply means that now you an xy basis attached to $p$. So you must draw once again two axis, which intersect at $p$, one parallel to the original $x$ axis, one parallel to the original $y$ axis. Now instead of projecting the vector $A$ (the same vector that you already drew) into the radial and angular axis, you project into the new $x$ and $y$ axis, and the numbers you will find for the coordinates are the numbers you computed $4.1$ and $9.18$.

You can put the vector $A$, all four axis and four projections into the same picture. Then the picture becomes self-explanatory. Note that you can draw the same picture for an arbitrary point $p$ and an arbitrary vector field $A$. This is in fact the standard way to represent vector fields in a plane, as searching 'vector field' in google images will certainly show. I hope I made myself clear.

Lucas SV.