- #1
Andy_K
Gold Member
- 39
- 5
Dear All,
I am doing the Special Relativity course at World Science U, and came across this question which I got wrong:
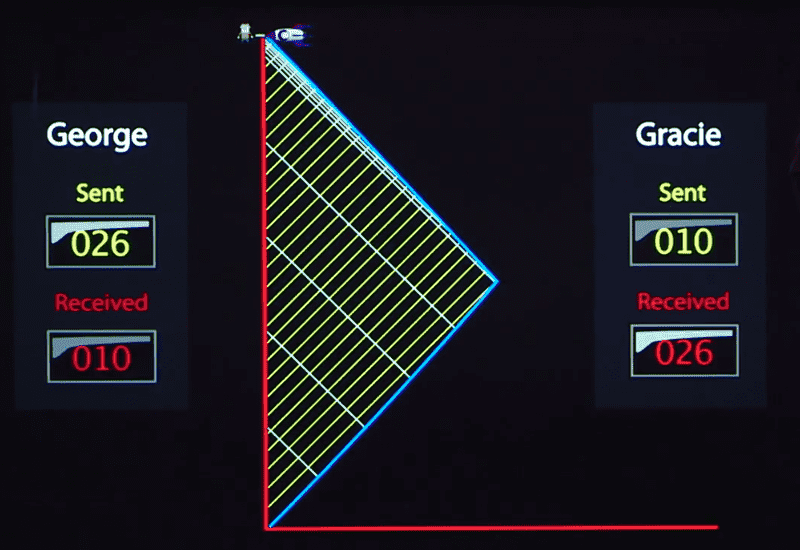
The answer is 170 ns. But I'm confused, shouldn't she observe 80 ns on George's earthbound watch (based on time dilation) at the turnaround moment? Based on the illustration from the course, it clearly shows that the light ray reaching the turnaround point is still from an older moment in time. Or am I misunderstanding the question?
Below is a diagram I'm referring to from his lecture video. Wouldn't Gracie only start seeing later moments of George along the journey back towards him?
 The lecture video of the above screenshot is as follows (starting at 7th minute):
The lecture video of the above screenshot is as follows (starting at 7th minute):
Can someone please enlighten me? Thank you.
I am doing the Special Relativity course at World Science U, and came across this question which I got wrong:
When 100 nanoseconds have elapsed on traveling Gracie's watch, she immediately stops, turns around, and heads back toward George at the same speed of her outbound journey, 3/5 light speed. Just as she starts the return journey, how much time will she say has elapsed on George's watch since the journey began?
The answer is 170 ns. But I'm confused, shouldn't she observe 80 ns on George's earthbound watch (based on time dilation) at the turnaround moment? Based on the illustration from the course, it clearly shows that the light ray reaching the turnaround point is still from an older moment in time. Or am I misunderstanding the question?
Below is a diagram I'm referring to from his lecture video. Wouldn't Gracie only start seeing later moments of George along the journey back towards him?
Can someone please enlighten me? Thank you.