Stephanus
- 1,316
- 104
Dear PF Forum,
After all these post'. I want to know that my understanding of twins paradox is close enough.
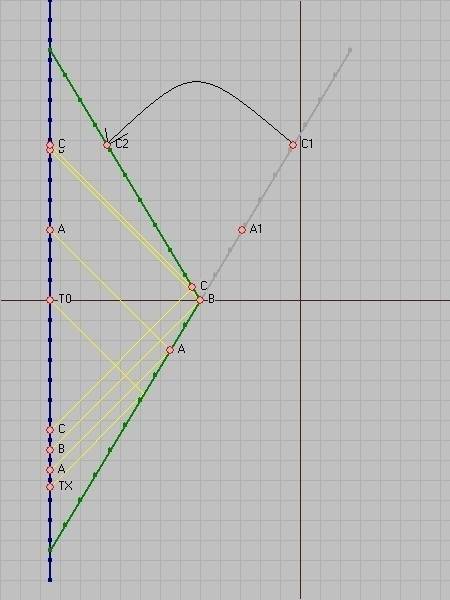
So, Green travels, Blue stays.
Blue keeps sending signal, Green bounces the signal.
Doppler factor = 1/4, so ##\frac{1}{4} = \frac{1-v}{1+v}; v = 0.6##
And at event T0 (from B), Green changes direction. Blue can calculate the doppler effect and position, and know that G is at B.
At event A (above) Blue thinks that Green is at A1. Blue never knows that Green has changed frame.
And at event C (above) while Blue thinks that Green is at C1, suddenly the Doppler factor changes. From 0.25 to 4. Then Blue realize that Green is not at C1 but at C2. That Green has suddenly jump from a distance to a spot at C2.
So it mustn't be Green. It's something else who looks like Green whose time is dilated, and now Green's clock is speeding up from event C (above) until they meet. But the speeding up can catch up Blue's clock.
So, nature cannot be fooled, but nature fools B.
And for Green, at event T0, Green will see that Blue whose time is dilated, but now Blue's clock is speeding up and catches up Green's clock and still going on until they meet.
Is this how Twins Paradox work?
After all these post'. I want to know that my understanding of twins paradox is close enough.
So, Green travels, Blue stays.
Blue keeps sending signal, Green bounces the signal.
Doppler factor = 1/4, so ##\frac{1}{4} = \frac{1-v}{1+v}; v = 0.6##
And at event T0 (from B), Green changes direction. Blue can calculate the doppler effect and position, and know that G is at B.
At event A (above) Blue thinks that Green is at A1. Blue never knows that Green has changed frame.
And at event C (above) while Blue thinks that Green is at C1, suddenly the Doppler factor changes. From 0.25 to 4. Then Blue realize that Green is not at C1 but at C2. That Green has suddenly jump from a distance to a spot at C2.
So it mustn't be Green. It's something else who looks like Green whose time is dilated, and now Green's clock is speeding up from event C (above) until they meet. But the speeding up can catch up Blue's clock.
So, nature cannot be fooled, but nature fools B.
And for Green, at event T0, Green will see that Blue whose time is dilated, but now Blue's clock is speeding up and catches up Green's clock and still going on until they meet.
Is this how Twins Paradox work?