mcleanrs
- 13
- 0
2 really tricky ones for me on this homework assignment. I think I got the other one settled (Thanks to help here) -- now I just need to finish this last one.
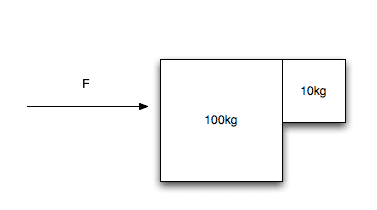
Two blocks sit on this frictionless table, but there is friction between the blocks.
Static = .589
Kinetic = .332
A = 100 kg
B = 10 kgWhat minimum force F must be exerted on A in order for B not to fall?
F=m•a
R - the static resistive force ---> fs*F=R
Attempt 1:
Since B isn't moving, I'll use the static friction force. I know that the force that A applies on B, times the static force, will be my upward force -- which I need to counter the downward force of gravity.
Since B is 10kg, I need 98 kg of up force.
98/589 = 166.4 N
So
Force to move block A = 980 N
Force to move block B = 98 N
980+98+166.4=1244 N
The only problem is I am given a range for the answer, and I need to be between 1700 and 2200, so I know that answer is wrong.
Once I find the force, then I'm supposed to find the overall acceleration...I think that should be easy, once I know the force.
Homework Statement
Two blocks sit on this frictionless table, but there is friction between the blocks.
Static = .589
Kinetic = .332
A = 100 kg
B = 10 kgWhat minimum force F must be exerted on A in order for B not to fall?
Homework Equations
F=m•a
R - the static resistive force ---> fs*F=R
The Attempt at a Solution
Attempt 1:
Since B isn't moving, I'll use the static friction force. I know that the force that A applies on B, times the static force, will be my upward force -- which I need to counter the downward force of gravity.
Since B is 10kg, I need 98 kg of up force.
98/589 = 166.4 N
So
Force to move block A = 980 N
Force to move block B = 98 N
980+98+166.4=1244 N
The only problem is I am given a range for the answer, and I need to be between 1700 and 2200, so I know that answer is wrong.
Once I find the force, then I'm supposed to find the overall acceleration...I think that should be easy, once I know the force.