Two blocks slide on an inclined plane

[hellovenus]

Homework Statement

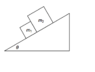
Two blocks slide on an incline of angle \theta . Block 1 has mass m1 and coefficient of kinetic friction μ1 with the surface, block 2 has mass m2 and coefficient of kinetic friction μ2. The gravitational acceleration is g.

In terms of these parameters, under what condition will the blocks remain in contact as they slide?

Homework Equations

ΣF_m1 = m₁gsinΘ- m₁g*μ1 = m1a
ΣF_m2 = m₂gsinΘ- m₂g*μ2 = m2a

The Attempt at a Solution

I am guessing that when the accelerations are both equal to zero, the blocks remain in contact? I am not sure under what conditions the blocks remain in contact with each other.[/B]

 

[haruspex]

under what condition will the blocks remain in contact

I assume there was a diagram showing them initially in contact, one above the other on the plane. Is that right? Which was higher?
What determines which would slide faster?

 

[hellovenus]

I assume there was a diagram showing them initially in contact, one above the other on the plane. Is that right? Which was higher?
What determines which would slide faster?

 

[haruspex]

View attachment 215295

Ok, so what about the answer to my last question?

 

[hellovenus]

Ok, so what about the answer to my last question?

I am not given the numerical values for any of the variables, and the question asks that under what conditions the blocks remain in contact with each other. Therefore I assume that m2 must slide faster than m1. m2 is higher according to the picture.

 

[haruspex]

I am not given the numerical values

Yes, I understand that.

assume that m2 must slide faster than m1.

Did you mean that? How can it overtake the lower block?

 

[hellovenus]

Yes, I understand that.

Did you mean that? How can it overtake the lower block?

I mean in order for the two blocks to stay in contact, m2 must have a higher or equal velocity compared to m1. If not, they would not be in contact? Right? If m2 has a "greater" velocity, it would mean that m1 and m2 would slide together? If that makes any sense...

 

[haruspex]

m2 must have a higher or equal velocity

Ok, you mean that it would have higher or equal velocity if they were side by side instead, right?

If m2 has a "greater" velocity, it would mean that m1 and m2 would slide together?

Yes, if m2 would otherwise have had the greater velocity they will slide together.
So do you wish to revise your answer to the question?

 

[chuuke]

I'm also trying to figure this problem out. I think have it, but am unsure of my answer.
For the blocks to stay in contact as they slide down, F₁≤F₂
Block m1:
Fnet_x1 = F_Nx-F_fx
F_f = μ₁F_N
F_N = F_gcosθ = m₁gcosθ
plugging into Fnet & F_f
Fnet_x1 = m₁gsinθ-μ₁m₁cosθ

Block m2:
Same equations as block m1 substituting in m2 mass and coefficient of friction μ2.

Since
F₁ ≤ F₂
then
Fnet_x1 = m₁gsinθ-μ₁m₁cosθ ≤ Fnet_x2 = m₂gsinθ-μ₂m₂cosθ
m₁g(sinθ-μ₁cosθ) ≤ m₂g(sinθ-μ₂cosθ)
therefore:

[m₁g(sinθ-μ₁cosθ)]/[m₂g(sinθ-μ₂cosθ)] ≤ 1

under this condition, the two blocks will remain in contact as they slide down the incline.

 

[haruspex]

For the blocks to stay in contact as they slide down, F1≤F2

How do you deduce that?

 

[chuuke]

How do you deduce that?

Wouldn't the acceleration of the m2 block have to be larger to push down the m1 block?

 

[haruspex]

Wouldn't the acceleration of the m2 block have to be larger to push down the m1 block?

Yes, but you wrote that the force is larger.

 

[Abhishek kumar]

Yes, but you wrote that the force is larger.

If we consider two block as a single block because in question it is given they remain in contact then acceleration would be same for both the block.

 

[haruspex]

If we consider two block as a single block because in question it is given they remain in contact then acceleration would be same for both the block.

Please see post #8. hellovenus seems to be happier thinking in terms of what the blocks would have done were they not in contact. Looks like chuuke also inclines to that way of thinking.