absolutezer0es
- 14
- 0
Here are two problems, both of which I'm not really sure where to start. The simpler (?) one first:
A 1.10-mm-diameter glass sphere has a charge of +1.10 nC. What speed does an electron need to orbit the sphere 1.80mm above the surface?
I thought of using v = (2*pi*r)/T because it is circular motion, but I can only derive "r" (I got r = 0.00235m, though I'm not sure if this is right. I know the sphere acts as a point charge and measured the 1.8mm and the radius of the sphere.). I don't feel like the electric field equations would get me anywhere.
Question 2 (and more complex):
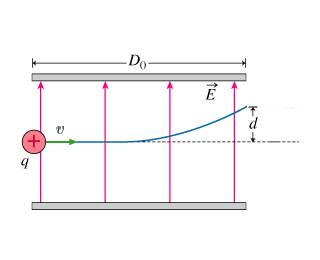
The ink drops have a mass m = 1.00×10−11kg each and leave the nozzle and travel horizontally toward the paper at velocity v = 22.0m/s . The drops pass through a charging unit that gives each drop a positive charge q by causing it to lose some electrons. The drops then pass between parallel deflecting plates of length D0 = 1.65cm, where there is a uniform vertical electric field with magnitude E = 8.10×104N/C .
If a drop is to be deflected a distance d = 0.250mm by the time it reaches the end of the deflection plate, what magnitude of charge q must be given to the drop? Assume that the density of the ink drop is 1000kg/m3 , and ignore the effects of gravity.
This one ... not a clue where to begin. I've got my electric field formulas ready to go. I'd appreciate any nudges you guys can give on either problem.
A 1.10-mm-diameter glass sphere has a charge of +1.10 nC. What speed does an electron need to orbit the sphere 1.80mm above the surface?
I thought of using v = (2*pi*r)/T because it is circular motion, but I can only derive "r" (I got r = 0.00235m, though I'm not sure if this is right. I know the sphere acts as a point charge and measured the 1.8mm and the radius of the sphere.). I don't feel like the electric field equations would get me anywhere.
Question 2 (and more complex):
The ink drops have a mass m = 1.00×10−11kg each and leave the nozzle and travel horizontally toward the paper at velocity v = 22.0m/s . The drops pass through a charging unit that gives each drop a positive charge q by causing it to lose some electrons. The drops then pass between parallel deflecting plates of length D0 = 1.65cm, where there is a uniform vertical electric field with magnitude E = 8.10×104N/C .
If a drop is to be deflected a distance d = 0.250mm by the time it reaches the end of the deflection plate, what magnitude of charge q must be given to the drop? Assume that the density of the ink drop is 1000kg/m3 , and ignore the effects of gravity.
This one ... not a clue where to begin. I've got my electric field formulas ready to go. I'd appreciate any nudges you guys can give on either problem.