Two Light Waves Through Plastic

[Dante Tufano]

So I'm on my last try for this question, and I could really use some help, I'm completely clueless..

Two waves of light in air, of wavelength λ = 460.0 nm, are initially in phase. They then travel through plastic layers as shown in Figure 35-36, with L1 = 4.00 µm, L2 = 3.50 µm, n1 = 1.20, and n2 = 1.60.

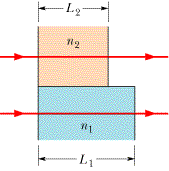
(a) What is their phase difference in cycles after they both have emerged from the layers and arrived at the same horizontal position?
_______________cycles
(b) If the waves at that later position are brought together to a single point, what type of interference occurs?

-closer to destructive interference
-cannot tell from the information given
-closer to constructive interference


2. I know that the change in phase is equal to (L/wavelength)(n-1)



3. I plugged in the given values, and got a phase shift of 4.565 radians for n2 and a shift of 1.739 radians for n1. These added to a shift of 6.304 radians. Since only the decimal matters, it's a shift of .304 radians. However, this is way off, since when I divide by 460nm to get the answer in terms of cycles, I get 661.63, which is wayyyy too large. Even then, I'm clueless on how to answer part b too. Can I please get some help?

 

[Dante Tufano]

Anybody? I really need help with this one..

 

[Dante Tufano]

Anybody?
The slightest help would be amazing

 

[rl.bhat]

Suppose, when the light enters the plastic sheet, the phase is zero.
The wavelength in the medium of n1 is 391.8 nm.
Number of waves in L1 is 4x10^-6m/391.8 nm. = 10.212
That means 10 full cycles plus 0.212 cycle. Hence phase difference is 0.212 cycle.
Now proceed.

 

[doogles8654]

Dante! Its a small world! This is Doug btw. I can't figure this one out for the life of me...