Two Spring System Homework: Find Distance & Max Velocity

[CAF123]

Homework Statement

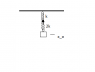
A box of mass m is released from rest at $x_o = 0$ with the two springs $k$ and $2k$ unstretched. Find the distance that the mass falls before rebounding. What maximum velocity does it obtain?

Homework Equations

Hookes law, gravitational force.

The Attempt at a Solution

Suppose the distance the top spring is stretched is $x_1$ and that of the lower spring, $x_2$. Then define $z = x_1 + x_2$. At equilibrium, $mg - 2kx_2 = 0$ and $2kx_2 = kx_1$. (There is an upwards force of $kx_1$ from the displacement of the upper spring and a downwards force of $kx_2$ since the extension of the lower spring causes a pull on the upper spring and by virtue of NIII, there is a corresponding reaction force). This means $x_1 = 2x_2$ so that $z = 3x_2$ and finally $mg - 2/3 k z = 0$ at equilibrium. So the system is equivalent to one with a spring constant of 2/3 and a displacement of the mass a distance z at equilibrium. In general, we can then write that the mass satisfies $mg - (2/3) k Z = m dv/dt$, where Z is some extension of the equivalent system with constant 2/3. Write this as $$g - \frac{2}{3} \frac{k}{m} Z = v\frac{dv}{dZ} \Rightarrow Zg - \frac{2}{3}\frac{k}{m} \frac{Z^2}{2} = \frac{v^2}{2}$$ so that $$v = \sqrt{2gZ - \frac{2}{3}\frac{k}{m}Z^2}$$ The distance the mass falls before rebounding is given by the first instant (other than at the point of release) when the velocity is zero. This implies $Z_{\text{before rebound}} = 3mg/k$ while maximum velocity is obtained from $dv/dZ = 0 \rightarrow Z = 3/2 (mg/k ).$. Is this correct?

 

[ehild]

It is correct, but you need to give the maximum speed, too.

ehild

 

[CAF123]

Hi ehild :)

It is correct, but you need to give the maximum speed, too.

ehild

Okay, so I evaluate v when Z = 3/2 mg/k. I was wondering if we could also solve this problem by writing explicit expressions for the displacement using a sin function for example. E.g writing Z = Asin(ωt) for example, but I am not really sure where to start with this analysis.

 

[ehild]

It will be a cosine function about the equilibrium position Ze=3/2mg/k.
If Z is the change of length of the two-spring system, and K is the equivalent force constant, $m\ddot Z = mg-KZ$ with the initial condition Z(0)=0. What is Z(t)?

ehild

 

[Chestermiller]

If two springs are in series, with spring constants k₁ and k₂, then, if they are supporting a force F, the total elongation is

Δx=\frac{F}{k_1}+\frac{F}{k_2}

So the overall spring constant, k=F/Δx is given by:

\frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}

Chet

 

[ehild]

Chet, that was explained and used in the solution in post #1.

ehild

 

[Gil]

You can use an energy approach to solve the velocity. You know the potential of both springs ($U=\frac{1}{2}kx^2$) and the mass. Just set $E= K + U$. When $V=0$ then $K=0$ and $E=U$ and when $V=max$ then $U=0$ and $E=K$.

 

[ehild]

@Gil: you forgot the gravitational potential energy.

Notice that the problem has been solved by the OP.

ehild

 

[Chestermiller]

Chet, that was explained and used in the solution in post #1.

ehild

Thanks ehild. I just wanted to show the relation in a more general way, and not just customized to this specific problem.

Chet

 

[CAF123]

Thanks ehild, I got it.

I solved this problem relative to the relaxed length of the spring. How would I do the same problem but with the analysis relative to the equilibrium length of the spring? For sure, $Z_{\text{equil}} = mg/K$ and I want to introduce a new coordinate $\tilde z$ such that this measures the extension of the spring from the point of equilibrium, mg/K. But I am having a bit trouble relating it to my initial coordinate $Z$, the coordinate from the relaxed length of the spring.

Many thanks.

 

[ehild]

Z_equil is the stretching at equilibrium. You previous variable Z is
$Z=\tilde z+Z_{equil}$.
$\ddot Z = \ddot {\tilde z}=mg-K(\tilde z+Z_{equil})$
but $Z_{equil}=mg/K$, it cancels and you are left with
$\ddot {\tilde z}=-K\tilde z$.

ehild

 

[CAF123]

Thank you.

I am trying to apply this to another related question. It is an example in some notes, so I have the solution in front of me but I am just trying to understand the step where they rewrite the motion relative to the point of equilibrium.

The description is 'A car moves with constant speed u along a road with vertical profile h(x), where h'(x) is small. The car is modeled by a chassis which keeps contact with the ground, connected to an upper mass m by a spring and a damper.' (see sketch)

From the notes: Let us denote by $Y(t)$ the vertical position of the mass relative to the ground and $\ell_o$ the natural length of the spring. Then the position of the mass is $Y = h + \ell_o + y$ so that the E.o.M of the mass relative to the ground is $m\ddot{Y} = -mg - k(Y-h-\ell_o)- \mu(\dot{Y} - \dot{h})$. This makes sense so far. Measuring $\tilde y$ from the equilibrium point, $-mg - k(Y-h-\ell_o) = -k(\tilde y-h)$. How was this derived?

I believe the set up is exactly analogous to that in the previous question, but with redefining the coordinate system so that the origin coincides with the ceiling for example. Analogously to what you wrote in the previous post, I write $Y = h + \ell_o + Y_{\text{equil}} + \tilde y$, where now I have the additional terms $h$ and $\ell_o$ since in this problem the origin is at the ground and not at the relaxed length as in the previous problem.

Then $\ddot{Y} = \ddot{\tilde y}$ (since h'(x) is small, ignore h''(x(t))) and $Y_{\text{equil}} = -mg/k + h + \ell_o$ Inputting this $Y, Y_{\text{equil}}$ back into the equation does not seem to give me the correct result. Any comments?

 

[ehild]

I can not follow you. I think the term with μ corresponds to damping, does it not?

Y(t) means the height of the mass measured from the ground. You got the equation m\ddot{Y} = -mg - k(Y-h-\ell_o)- \mu(\dot{Y} - \dot{h}).As h also changes, do not include it into Y_equil. The book defines it as $Y_{equil}=\ell_o-\frac{mg}{k}$ and $\tilde y = Y- Y_{equil}$.
Then -mg - k(Y-h-\ell_o) =-mg - k(Y_{equil}+\tilde y-h-\ell_o)=-mg - k(\ell_o-\frac{mg}{k}+\tilde y-h-\ell_o) =-k(\tilde y-h) and the differential equation becomes

m\ddot{\tilde y}=-k(\tilde y-h)-\mu(\dot{\tilde y}-\dot h)

ehild

 

[CAF123]

I can not follow you. I think the term with μ corresponds to damping, does it not?

Yes, sorry I see that wasn't made clear.

The book defines it as $Y_{equil}=\ell_o-\frac{mg}{k}$ ...

Why is this the case? I see that it solves the problem, but from the original eqn $m\ddot{Y} = ...$, when I set $\ddot{Y}=0$ and solve for $Y_{\text{equil}}$, I obtain $\ell_o - mg/k + h$.

Thanks.

 

[ehild]

They can define Y_equil this way. It is just the equilibrium length of the spring in gravitational field. It would have been better to name it something else.
h(x) (x is the horizontal coordinate) is given and it changes as the car moves, and the motion of the mass will depend on h(x) . I think the problem goes forward by assuming that the car travels with some speed and find its vertical motion.

ehild