Two stacked blocks, push using one block, static friction between blocks

[dammitpoo]

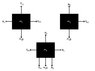
Newtonian mechanics problem with blocks

Problem:

m_{1} and m_{2} each interact with m_{3} via static friction, with the same \mu_{s}. The horizontal surface below m_{3} is frictionless. An external force F_{ext} acts on m_{1} from the left and the entire system of three connected masses moves to the right (and obviously accelerates). The idea is to provide a suitable magnitude of F_{ext} as to prevent both m_{1} and m_{2} from moving with respect to m_{3} during the acceleration, i.e. we don’t want m_{1} to slide down along, nor m_{2} to slide “back” along m_{3}. To make life easy, we let m_{1}, m_{2} and m_{3} all have the same mass m.

a) Find in terms of relevant parameters, the possible range of F_{ext} which will allow the desired motion to take place.
b) It might be that, if \mu_{s} is less than some critical value \mu_{s(critical)}, no value of F_{ext} will allow the desired motion. Give a simple argument why this might be true, and if so, determine \mu_{s(critical)} in terms of relevant parameters.

Relevant equations:

\sum F = ma

Here is my attempt at the problem:

Part A:
For m_{2}:
N_{2} = m_{2}g
F_{fr2} = m_{2}a
\mu_{s}m_{2}g = m_{2}a
\mu_{s}g = a
\mu_{s} = \frac{a}{g}

For m_{1}:
F_{ext} - N_{1} = m_{1}a
N_{1} = F_{ext} - m_{1}a
F_{fr1} = m_{1}g
\mu_{s} (F_{ext} - m_{1}a) = m_{1}g

For m_{3}:
N_{3} - F_{fr1} - N_{2} = m_{3}g
N_{1} - F_{fr2} = m_{2}a

Substitute in for N_{1} and F_{fr2}:
N_{1} - \mu_{s}m_{2}g = m_{2}a
F_{ext} - m_{1}a - \mu_{s}m_{2}g = m_{2}a
F_{ext} = m_{3}a + m_{1}a + \mu_{s}m_{2}g

Since \mu_{s}m_{2}g = m_{2}a:
F_{ext} = m_{3}a + m_{1}a + m_{2}a

Since m_{1} = m_{2} = m_{3} = m:
F_{ext} = 3ma

Part B:
My guess is that if \mu_{s} is infinitely small so that friction is negligible, any magnitude of force applied on the blocks would cause block 1 to slide down and block 2 to slide backwards relative to block 3.

I don't know where to start with the parameters, but here is what I have so far:
\mu_{s(critical)} < \mu_{s}
F_{fr(critical)} < F_{ext} < F_{fr}

Any help would be highly appreciated!

 

[kuruman]

You have found the common acceleration fo the three masses, $a=\dfrac{F_{ext}}{m_1+m_2+m_3}.$ That's a good start. Then you can find $F_{h2}$ because it is the net force on $m_2$, $$F_{h2}=m_2a=\frac{m_2F_{ext}}{m_1+m_2+m_3}$$Using similar reasoning you can find the rest of the internal horizontal forces between blocks. The internal vertical forces are easy to find because there is no vertical acceleration. Once you have all the intrnal forces, you can set up the threshold inequalities.