ca2n
- 10
- 0
Hello all,
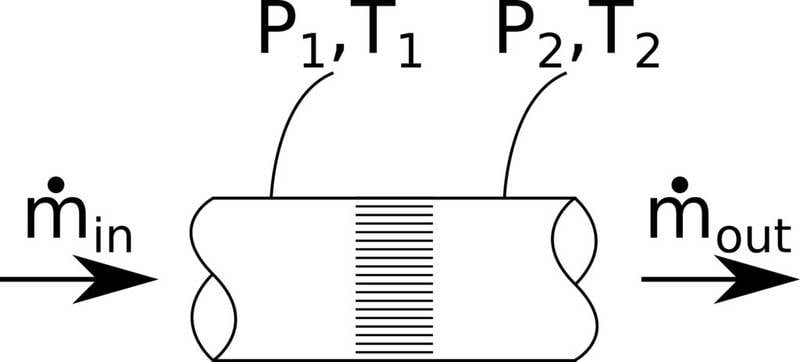
I have an in-house designed flow meter with roughly the configuration in the figure. In the setup, a restriction is placed in the flow stream (the rows of horizontal lines in the figure). Pressure measurements upstream and downstream of the restriction, P1 and P2, respectively are continuously monitored.
For calibration (determining the relationship between P1-P2 and the mass flow rate), the air flowing through the system is supplied to a nozzle with a flow straightener upstream of the nozzle exit. Velocity measurements with hot-wire anemometry allows me to calculate the mass flow rate at the exit of the nozzle at discrete P1-P2 values.
So that's how far the calibration goes. Now on to how it's used in experiments.
For some of the experiments that I am conducting there can be a rather significant resistance in the flow (a filter). The backpressure created by this resistance is monitored by a pressure gauge mounted just upstream of P1 and may reach up to 1 bar (gauge). I am uncertain as to how this backpressure affects the flowmeter calibration. For example:
Let's say from the flow meter calibration, a mass flow rate, m-dota is provided by P1-P2 = Pa.
If a resistance is fitted downstream, causing backpressure, is m-dota still provided by Pa?
Thank you in advanced for any response.
I have an in-house designed flow meter with roughly the configuration in the figure. In the setup, a restriction is placed in the flow stream (the rows of horizontal lines in the figure). Pressure measurements upstream and downstream of the restriction, P1 and P2, respectively are continuously monitored.
For calibration (determining the relationship between P1-P2 and the mass flow rate), the air flowing through the system is supplied to a nozzle with a flow straightener upstream of the nozzle exit. Velocity measurements with hot-wire anemometry allows me to calculate the mass flow rate at the exit of the nozzle at discrete P1-P2 values.
So that's how far the calibration goes. Now on to how it's used in experiments.
For some of the experiments that I am conducting there can be a rather significant resistance in the flow (a filter). The backpressure created by this resistance is monitored by a pressure gauge mounted just upstream of P1 and may reach up to 1 bar (gauge). I am uncertain as to how this backpressure affects the flowmeter calibration. For example:
Let's say from the flow meter calibration, a mass flow rate, m-dota is provided by P1-P2 = Pa.
If a resistance is fitted downstream, causing backpressure, is m-dota still provided by Pa?
Thank you in advanced for any response.