Roger900
- 11
- 0
Hello Physics Specialists,
I am having some difficulty understanding the Work Equation with respect to the Cosine Theta portion of the equation.
Work = Force * Distance * Cosine(theta)
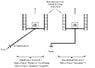
Attached is a picture of two hypothetical mechanical devices. I understand how to calculate work for the device on the left side of the page. However, the device on the right side of the page is more confusing. With this device, the force is directed towards the same direction of travel of the linear bearing slides, but the force is being applied on an offset to direct linear travel. And here is the problem...because of the offset pushing motion, the "arms" of the device will want to push clockwise against the side walls of the linear bearing assembly. Is Cosine(theta) involved here, or just friction from pushing on the side walls? What would be the math formula to calculate work?
Thanks,
Roger
I am having some difficulty understanding the Work Equation with respect to the Cosine Theta portion of the equation.
Work = Force * Distance * Cosine(theta)
Attached is a picture of two hypothetical mechanical devices. I understand how to calculate work for the device on the left side of the page. However, the device on the right side of the page is more confusing. With this device, the force is directed towards the same direction of travel of the linear bearing slides, but the force is being applied on an offset to direct linear travel. And here is the problem...because of the offset pushing motion, the "arms" of the device will want to push clockwise against the side walls of the linear bearing assembly. Is Cosine(theta) involved here, or just friction from pushing on the side walls? What would be the math formula to calculate work?
Thanks,
Roger