Understanding Inductance and Induced EMF in Simple Circuits

[TSny]

[The following is for fun and to check my understanding. If inappropriate in any way, please delete.]

Joline and Tim are considering a circuit that consists of an inductor of inductance $L$ and a load resistor of resistance $R$. Unlike an ideal inductor, the coils of the inductor in this circuit have a non-negligible total resistance $R_C$. At time $t = 0$, there is a current $I_0$ in the direction shown and the current is decreasing. They want to work out the current as a function of time.

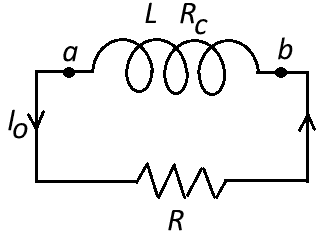
The two are arguing about which point $a$ or $b$ is “at the higher potential”. Joline claims $a$ must be at the higher potential to drive current through the load resistor $R$ in the given direction. Tim disagrees, saying that $b$ must be at the higher potential to push current through the resistance $R_c$ of the inductor in the given direction.

They decide to visit their professor to find out who is right. Professor L. smiles and says, “You two have a conundrum because you both believe that ’potential at a point of this circuit' has meaning. It doesn’t. You don’t need to consider potential at all. Electric field is what pushes the charge carriers. Just use Faraday’s law!” $$\oint \mathbf{E}\cdot \mathbf{ds} = -\frac{d \Phi}{dt}.$$
Joline and Tim agree to try this. For the closed path of the integral of the electric field, they choose a path that goes once around the circuit in the direction of the current and the path stays within the conducting material of the circuit. (So, the path through the inductor follows the corkscrew windings of the inductor.) They see that the rate of change of magnetic flux through this path of integration can be expressed as $\large \frac{d \Phi}{dt} = L\frac{dI}{dt}$. Assuming that the hookup wire connecting the inductor to the load resistor has negligible resistance, they write Faraday’s law as $$\oint \mathbf{E} \cdot \mathbf{dl} = \left(\int \mathbf{E}\cdot \mathbf{ds}\right)_{\rm through \, load}+\left(\int \mathbf{E}\cdot \mathbf{ds}\right)_{\rm through \, inductor} = -L\frac{dI}{dt}.$$ From Ohm’s law, the integrals through the load and the inductor can be written as $IR$ and $IR_C$, respectively. Making these substitutions and rearranging, Joline and Tim agree that the differential equation that determines the current as a function of time is $$\frac {dI}{dt} = -\frac{R + R_C}{L} I.$$ From this they derive easily the current as a function of time.

 

[hutchphd]

Looks good to me. No muss, no fuss, no auxiliary fields or magic wires : only Maxwell (Faraday closed loop integral version) required. A required bedtime story for all budding physicists....and EE's

 

[Delta2]

So no one wants to hear from me the full treatment of this I have in mind using Maxwell's equation's the differential version of Ohm's law and concepts like scalar potential, vector potential, conservative and non conservative fields?

 

[Charles Link]

I think @TSny 's is a good question, but it is a trick question. You need to ask, how did it achieve these initial conditions? It appears it would have been necessary to run a (e.g. a DC) voltage source from "b" to "a" without the resistor $R$ in the circuit, in order to establish the current in the inductor. Then at time t=0, the voltage source is removed and the resistor attached. Upon doing so, an EMF occurs in the inductor from "b" to "a" to try to maintain the current, and so from then on "a" is at the higher voltage.

 

[hutchphd]

So no one wants to hear from me the full treatment of this I have in mind using Maxwell's equation's the differential version of Ohm's law and concepts like scalar potential, vector potential, conservative and non conservative fields?

Finite size wires? Non-ideal inductor? Non-uniform currents? Relativistic delays? There are no easy closed form exact solutions. You need to be judiciously approximate.....which means quantifying each assumption.

 

[hutchphd]

but it is a trick question

It sure fooled me.

It appears it would have been necessary to run a (e.g. a DC) voltage source from "b" to "a" without the resistor R in the circuit, in order to establish the current in the inductor.

This is called a "switch". Sorry but this is silly and I am finished.

 

[TSny]

You need to ask, how did it achieve these initial conditions?

Imagine a bar magnet partially inserted into the coil. Then yank the magnet out. This will induce a current in the circuit. Let $t = 0$ be some instant after the magnet has been pulled out but before the current has completely died away.

 

[Charles Link]

So no one wants to hear from me the full treatment of this I have in mind using Maxwell's equation's the differential version of Ohm's law and concepts like scalar potential, vector potential, conservative and non conservative fields?

See the recent https://www.physicsforums.com/threads/inducing-emf-through-a-coil-understanding-flux.940861/page-4 which you apparently missed,
starting around post 36 and on to 58 and then on to many more posts, but be sure and see post 107. We really gave it a very thorough discussion. It never got complete acceptance, but I think we made a reasonable case for some of the calculations involving a separation of $E_{induced}$ and $E_c$ (electrostatic). I don't know that much more can be added to the discussion other than there will be those who agree, and perhaps some who strongly disagree.

 

[PhDeezNutz]

So no one wants to hear from me the full treatment of this I have in mind using Maxwell's equation's the differential version of Ohm's law and concepts like scalar potential, vector potential, conservative and non conservative fields?

I certainly would.

 

[Charles Link]

Imagine a bar magnet partially inserted into the coil. Then yank the magnet out. This will induce a current in the circuit. Let $t = 0$ be some instant after the magnet has been pulled out but before the current has completely died away.

"a" will be at the higher voltage. The EMF is from "b" to "a". (Here I'm localizing the EMF, which may be against the rules that it often goes by="that there is an EMF in the circuit loop, but you can't specify where").

I do disagree with the rule in a number of cases, the inductive coil being a good example where the rule is used as the reason they disagree with having an $E_{induced}$ and $E_c$. Instead, the $E_{induced}$ is given the freedom to go wherever in the circuit they need to place it.

 

[Delta2]

I am really annoyed by how @hutchphd quite often uses his intelligence for the purpose of irony.

 

[Charles Link]

The issue though is does the physics of an $E_{induced}$ and $E_c$ have some merit, which I believe it does, or is the Faraday circuit law with the traveling EMF (able to go where it is needed) the best we can do?

 

[Delta2]

I certainly would.

Fine thanks.

My main point is that the question asks for the scalar potential which is due to the conservative E-field which has as source the surface charge densities in the wires of the coil and that the EMF of the coil due to the decreasing current is due to the vector potential (that is generated by the time varying current according to the retarded potential equation) and the non conservative E-field.

If you want to hear more tell me.

 

[Charles Link]

If you want to hear more tell me.

One suggestion would be to add your inputs to the thread that I linked in post 38. The topic is really too advanced for the Introductory Physics Homework section.

 

[DaveE]

...it is a trick question. You need to ask, how did it achieve these initial conditions?

Really? You have to know the past to describe the future?

One of the really nice things about linear systems is that you don't have to ask "how did the ICs come about". You may, if you chose, just accept them as the initial state of the system and derive the future behavior from that point. The OP never asked about behavior before $t=0$.

Specifying ICs without describing history isn't a trick, it's common in the EE world as a practical application of the concept of "state". In fact history is quite irrelevant for idealized linear systems.

 

[DaveE]

So no one wants to hear from me the full treatment of this I have in mind using Maxwell's equation's the differential version of Ohm's law and concepts like scalar potential, vector potential, conservative and non conservative fields?

I don't think the OP does. This all stated as a simple question about the ideal (lumped element) behavior of inductors. Maybe y'all should argue with each other in another thread... again.

 

[Delta2]

I don't think the OP does. This all stated as a simple question about the ideal (lumped element) behavior of inductors. Maybe y'all should argue with each other in another thread... again.

Ye ok I knew from the start that my explanation with scalar and vector potential and .. surface charge densities is way too much for a college level problem.

 

[Charles Link]

Really? You have to know the past to describe the future?

I thought I did ok for a quick response. If you look at the post 31 again, Tim gave a fairly good reason for why "b" needed to be at a higher voltage. Looking at it closer, that higher voltage at "b" looks like it occurs before time t=0.

People seem to be starting to chew at each other a little here=it might do well to give it a break and get a cup of coffee. Cheers. :)

 

[DaveE]

Whatever your argument about the complex mysteries of EM. Make sure they agree with reality. Now days you don't even need to go into the lab to do that.

 

[Charles Link]

The problem at hand in this thread is the post by the OP. It should be noted that the $E_{induced}$ in an inductor runs in the same direction as the EMF in a battery, with the EMF pointing to the positive voltage point. I like @kuruman 's diagrams and explanation.

Meanwhile the problem posted by @TSny is interesting, and also fairly easy to solve. I think we are probably all in agreement that the positive voltage is at the "a" end.

Back to the problem posted by the OP, it is of interest how the $E_{induced}$ behaves differently from an electrostatic $E$ such as when you have capacitor plates that are charged=the plus voltage end is found in the direction that the $E$ field is pointing from. @kuruman does have a very good explanation (post 24) and hopefully the OP also found it to be a good one.