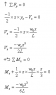Understanding Shear and Bending Moments in Beam Analysis

[jofree87]

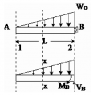
I have the solution's manual for this particular problem, but I'm having hard time understanding the steps they've taken. I've attached pictures of the problem below.

For the shear, are they using 1/2*x*(wx/L) because it is equal to the area of the force?

And for the bending moment, where are they getting x/3 from? is that the from the centroid's distance?

 

[PhanthomJay]

Yes to both questions. The triangularly distributed load has a load intensity of W_o(x/L). They are cutting a section of the beam a distance x from the left end in a free body diagram of the left cut portion of the beam, then summing forces = 0 and summing moments about the cut section = 0.