TheBC said:
But the big advantage of loedel diagram is that all time and space units have equal length. This makes reading reciprocal time dilation and length contraction as a result of relativity of simultaneity in 4D spacetime a lot easier.
Maybe you could show us how it is a lot easier.
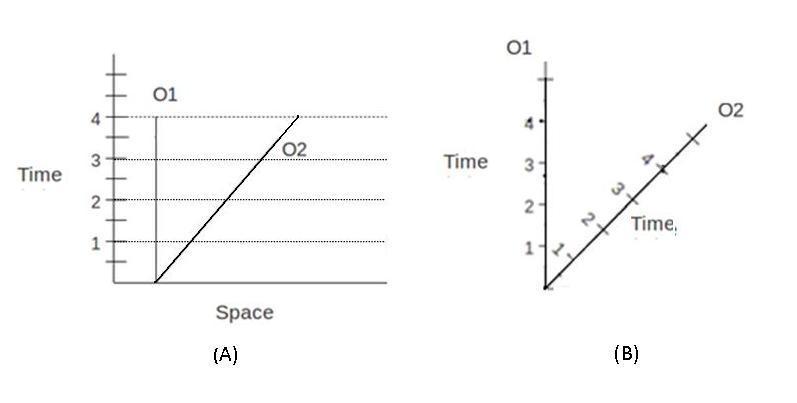
Here is a spacetime diagram showing two spacecraft departing from each other at the same opposite speed of 0.6c in this Inertial Reference Frame (IRF). I'm defining the speed of light to be 1 foot per nanosecond. The dots represent 1 microsecond intervals of Proper Time along each worldline:
Note that the spaceships are both 4000 feet long in this IRF.
However, if we look at the IRF corresponding to the rest frame of the Black&Blue spaceship, we see that its Proper Length is 5000 feet:
We can also easily see the Time Dilation of the Red&Green spaceship by dividing the Coordinate Time of 17 usec by the Proper Time of 8 usec for the top red dot yielding a Time Dilation factor of
2.125 which also the value of gamma for a speed of 0.882353 (the relativistic sum of 0.6c and 0.6c).
We can take the inverse of gamma, 1/2.125 = 0.471 to confirm that the Length Contraction of the Red&Green spaceship is 5000 times 0.471 or
2353 feet. At the Coordinate Time of 17 usecs, we can see that the green line is 2353 feet further to the right than the top red dot.
Here is the IRF in which the Red&Green spaceship is at rest:
And we can confirm that the Time Dilation and Length Contraction factors are reciprocal, that is, in the rest frame of each spaceship, the other spaceship is Time Dilated and Length Contracted to the same degree.
Can you please show us how the first diagram shows these effects any easier than the other two diagrams?