Understanding the concept of voltage

[luca54]

Hi everyone!

I ask some help in understanding better the concept of voltage. The voltage is a difference in electric potential between two points $a$ and $b$. It is defined as

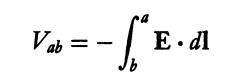
However, I'm a bit confused with the use of notation:

- Is $V_{ab}$ the same as $\Delta{V}$, or rather $-\Delta{V}$? In fact, $V_{ab}$ is also written as $V_a-V_b$, while $\Delta{V}$ should be a difference between a final and an initial position.
- What do $a$ and $b$ represent? They are extrema of integration, but how do we select them in a problem, one as the starting position and the other as the arrival? What does the integration from one to the other (and not vice versa) mean?

Eventually, I would like to add another question, this one about the integrand:

- What is concretely $dl$, and what is its direction?

Thanks very much!

 

[Dale]

Looks like you are copy-pasting from stack exchange. For inline LaTeX you have to replace the SE $ with the PF ##

I reverted and updated for you

 

[luca54]

Ah thanks a lot!
Yes, I've posted the question also there, but it hasn't been directly answered, and my doubts are still there

 

[Lord Jestocost]

Maybe, this migt be of help: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elewor.html

 

[vanhees71]

This is only true for electrostatics, because only then the electric field has a potential, independent of the integration path in your formula, i.e., you can use any path connecting the points with the position vectors $\vec{x}_a$ and $\vec{x}_b$. The potential is defined as
$$V(\vec{x})=-\int_{C(\vec{x}_0,\vec{x})} \mathrm{d} \vec{r} \cdot \vec{E}(\vec{r}),$$
where $C(\vec{x}_0,\vec{x})$ is an arbitrary curve connecting an arbitrary fixed point $\vec{x}_0$ with the variable point $\vec{x}$. Then you have
$$\vec{E}(\vec{x})=-\vec{\nabla} V(\vec{x}).$$
The voltage is simply the difference of the potentials between the two points in question,
$$\Delta V=V(\vec{x}_b)-V(\vec{x}_a).$$
Since the line integral defining $V$ only depends on the initial an final points of the path, you get
$$\Delta V=-\int_{C'(\vec{x}_a,\vec{x}_b)} \mathrm{d} \vec{r} \cdot \vec{E}(\vec{r}),$$
where $C'(\vec{x}_a,\vec{x}_b)$ is an arbitrary path connecting the points at $\vec{x}_a$ and $\vec{x}_b$.

 

[luca54]

Maybe, this migt be of help: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/elewor.html

Thanks very much!

 

[luca54]

This is only true for electrostatics, because only then the electric field has a potential, independent of the integration path in your formula, i.e., you can use any path connecting the points with the position vectors $\vec{x}_a$ and $\vec{x}_b$. The potential is defined as
$$V(\vec{x})=-\int_{C(\vec{x}_0,\vec{x})} \mathrm{d} \vec{r} \cdot \vec{E}(\vec{r}),$$
where $C(\vec{x}_0,\vec{x})$ is an arbitrary curve connecting an arbitrary fixed point $\vec{x}_0$ with the variable point $\vec{x}$. Then you have
$$\vec{E}(\vec{x})=-\vec{\nabla} V(\vec{x}).$$
The voltage is simply the difference of the potentials between the two points in question,
$$\Delta V=V(\vec{x}_b)-V(\vec{x}_a).$$
Since the line integral defining $V$ only depends on the initial an final points of the path, you get
$$\Delta V=-\int_{C'(\vec{x}_a,\vec{x}_b)} \mathrm{d} \vec{r} \cdot \vec{E}(\vec{r}),$$
where $C'(\vec{x}_a,\vec{x}_b)$ is an arbitrary path connecting the points at $\vec{x}_a$ and $\vec{x}_b$.

Thanks very much for the answer!

 

[Dale]

What does the integration from one to the other (and not vice versa) mean?

Since you have responses about the other portions, I thought I would address this. If you have a typical voltmeter then A will be your red lead wire and B will be your black lead wire. So integrating from A to B or from B to A is just a matter of switching your lead wires.