OliskaP
- 38
- 7
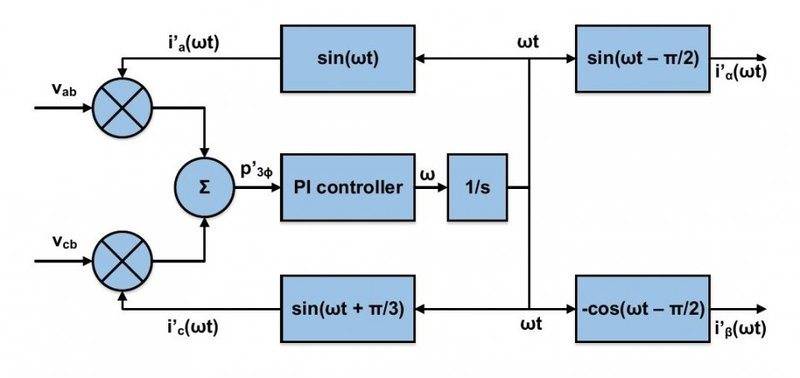
I have some trouble fully understanding the PLL block diagram shown below in the figure. The PLL circuit is used to generate currents (i alpha and i beta) which are in phase with the positive fundamental sequence of the voltage.
I am using the book "Instantaneous Power Theory and Applications to Power Condition" which I found as a pdf on the web.
The authors write:
The author also write that the frequency \omega has to be equal to the system frequency and the current and voltages has to be orthogonal to reach a stable point of operation.
Why must \omega be equal to system frequency to reach a stable point of operation?I would appreciate if someone help me fully understood how this circuit works
EDIT: I forgot to write 2pi/3 at the left bottom block, i wrote pi/3.
I am using the book "Instantaneous Power Theory and Applications to Power Condition" which I found as a pdf on the web.
The authors write:
- The only way for the PLL to reach a stable point is if the input to the PI controller in steady state has an average value of zero.
The author also write that the frequency \omega has to be equal to the system frequency and the current and voltages has to be orthogonal to reach a stable point of operation.
Why must \omega be equal to system frequency to reach a stable point of operation?I would appreciate if someone help me fully understood how this circuit works
EDIT: I forgot to write 2pi/3 at the left bottom block, i wrote pi/3.