Understanding Total Voltage in Parallel Circuits

[physics_CD]

Homework Statement

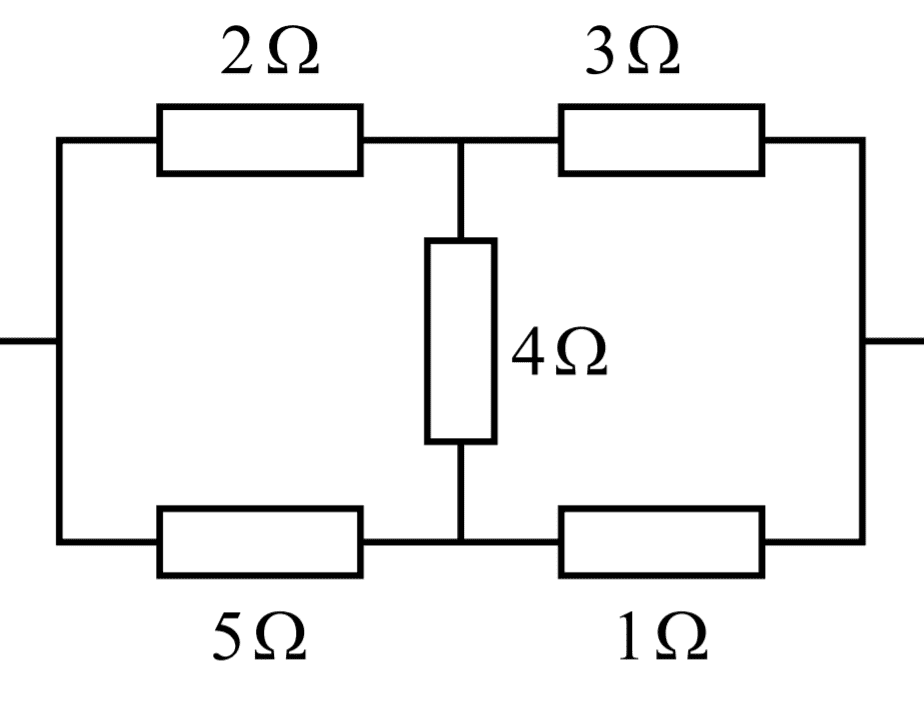
I have this resistor which is connected to some battery (not very important). I don't understand why the total voltage is equal to the voltage drop over the 3 Ω and 2 Ω resistors. Why is it not dependent on the resistor in the middle with 4 Ω . I do understand it if the 4 Ω were substituted with a wire. But how can it be that there is no difference whether it is 4 Ω or 0 Ω?

Relevant Equations

.

I really don't have any clue why the total voltage is equal to the voltage drop over the 3 Ω and 2 Ω resistors and independent of the 4 Ω resistor . Does it have to do with parallel circuits?

 

[phinds]

And just where are you applying the voltage. Your circuit is incomplete without showing that. I assume it's on the far left and far right but you need to say. Draw the circuit WITH the power source.

 

[physics_CD]

And just where are you applying the voltage. Your circuit is incomplete without showing that. I assume it's on the far left and far right but you need to say. Draw the circuit WITH the power source.

Yes it is the far left and far right. I am sorry for not mentioning it.

 

[etotheipi]

There are a few ways of thinking about it. Suppose the potential on the far left is A volts, the potential at the node between the $2\Omega$ and $3\Omega$ resistors is B volts, and the potential on the far right is C Volts. Then the magnitude of the change in potential tracing along the very top loop is the sum of the individual changes: $(A-B) + (B-C) = A-C$.

This is similar to how Kirchoff's law is formulated, though we would need to have a closed loop like @phinds mentioned to apply it, with the power source connected to the far left and far right.

 

[physics_CD]

There are a few ways of thinking about it. Suppose the potential on the far left is A volts, the potential at the node between the $2\Omega$ and $3\Omega$ resistors is B volts, and the potential on the far right is C Volts. Then the magnitude of the change in potential tracing along the very top loop is the sum of the individual changes: $(A-B) + (B-C) = A-C$.

This is similar to how Kirchoff's law is formulated, though we would need to have a closed loop like @phinds mentioned to apply it, with the power source connected to the far left and far right.

But there are different ways I can go from A to B. Does this mean that the voltage drop is independent of which path I choose to go? (I assume that I can't go over the same path)

 

[etotheipi]

But there are different ways I can go from A to B. Does this mean that the voltage drop is independent of which path I choose to go? (I assume that I can't go over the same path)

Yes. The magnitude of the potential difference between the two end points is $A-C$, since that is what we've labeled them. Now if we trace along any possible path from one end to the other, and add up all of the changes in potential as we go, we'll always end up with this value. It is a property of a conservative field that the change in potential energy is only dependent on the start and end points.

Of course, if want to start figuring out the currents through individual components, we will need to work out the potentials at some of the nodes in the middle.

 

[phinds]

@physics_CD you are seriously overthinking this. If you have a battery hooked to the far left and far right, WHY would you expect the voltage of the battery to be effected by the value of the resistors (unless they were ALL zero in which case you'd have a short circuit)?

IF you would just DRAW the battery the way I asked I think it might be more clear to you.