Uniform electric field interaction

[kvanr]

Homework Statement

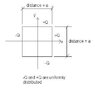
Electric charge is distributed along each side of a square. Two adjacent sides have positive charge +Q on each, two sides have -Q on each.

What are the x and y components of the net electric field at the center of the square? (Each side has length "a").

Homework Equations

E=F/q ?
F=k*q1*q2/r^2
k=9E9Nm^2/C^2

The Attempt at a Solution

Trying to come up with a differential equation? I don't know how to begin with having 4 sides.

 

[marcusl]

You need the formula for the electric field from a charge (look in your book). Then argue from the special symmetry at the center of the square.

 

[kvanr]

You need the formula for the electric field from a charge (look in your book). Then argue from the special symmetry at the center of the square.

You mean the diagonal symmetry?

edit: Then that would make it equal 0 at the center?
I was thinking it was zero?

 

[marcusl]

Well, pick a side (say the top) and integrate the field at the center as you move the source point along (left to right). Mentally summing the vectors (look at the symmetry) will show you the net direction even without doing the math. Now that you know the answer for one side, it's straightforward to add the contributions of other three.

Hint: the field is not 0 at the center.