iRaid
- 558
- 8
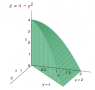
Homework Statement
Use a double integral to find the volume of the indicated solid.
Homework Equations
The Attempt at a Solution
I can't find what I did wrong, it seems like a simple problem...
$$\int_0^2 \int_0^x (4-y^{2})dydx=\int_0^2 4x-\frac{x^{3}}{3}dx$$
$$=2x^2-\frac{x^{4}}{12}|_0^2=8-\frac{16}{12}=\frac{20}{3}$$