ipat918
- 2
- 0
- Homework Statement
- Use a variable substitution to get into a Bessel equation form?
- Relevant Equations
- Bessel equation
Hello,
For my homework I am supposed to get-
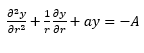
into the form of a Bessel equation using variable substitution. I am just not sure what substitution to use.
Thanks in advance.
For my homework I am supposed to get-
into the form of a Bessel equation using variable substitution. I am just not sure what substitution to use.
Thanks in advance.