lmstaples
- 31
- 0
Homework Statement
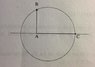
The line segment AB lies on a diameter of a circle of radius 1, and the angle BAC is a right angle.
Find the greatest possible value of the sum of the lengths of AB and AC.
Homework Equations
The Attempt at a Solution
I have no idea what parameters to use or how to set up the problem.
Any help would be much appreciated.