Variable Magnetic field bound in a cylindrical region

[Saitama]

Homework Statement

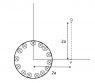
There is a uniform but variable magnetic field $\vec{B}=(B_0 t)(-\hat{k})$, in a cylindrical region, whose boundary is described by $x^2+y^2=a^2$. $\displaystyle \int_P^{Q} \vec{E} \cdot \vec{dy}$ is (see attachment 1)
A)0
B)$\frac{\pi}{4}(B_0 a^2)$
C)$-\frac{\pi}{8}(B_0 a^2)$
D)$\frac{\pi}{8}(B_0 a^2)$

Homework Equations

The Attempt at a Solution

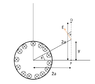
(see attachment 2)
The electric field produced will be in anticlockwise direction. At a distance y from P, the electric field can be calculated using Gauss's law.
$$E \cdot 2\pi \sqrt{4a^2+y^2}=B_0 \pi a^2$$
$$E=\frac{B_0 a^2}{2\sqrt{4a^2+y^2}}$$

Since y is in the vertical direction, we need to only consider the vertical component to evaluate the integral asked in the question.
$$\int_{P}^{Q} \vec{E}\cdot \vec{dy}=\int_0^{2a} E\cos \theta dy$$
$$=\int_0^{2a} \frac{B_0 a^2}{2\sqrt{4a^2+y^2}} \cdot \frac{2a}{\sqrt{4a^2+y^2}} dy$$

Solving the integral, I get D which is correct.

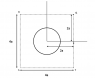
The problem is I don't understand what the solution booklet has mentioned. The solution goes like this: (see attachment 3)

$$\int_{P}^Q \vec{E} \cdot \vec{dy}=\frac{1}{8}[\vec{E} \cdot \vec{dl} \text{ for square } TQRST]$$
$$=\frac{1}{8} \frac{d[\pi a^4B_0t]}{dt}$$
$$=\frac{\pi}{8}B_0 a^2$$

I don't understand how they even got the first two steps.

Any explanation on this would be helpful. Thanks!

 

[BBAI BBAI]

See the line integral from P to Q is one eight of the whole perimeter of the square...So the first line is written..It is similar like the electric flux concept which we use...In the second line...it should be a^2

 

[Saitama]

See the line integral from P to Q is one eight of the whole perimeter of the square...So the first line is written..It is similar like the electric flux concept which we use...In the second line...it should be a^2

Yes, it should be a^2, sorry for the typo but I am not yet able to understand why the method works.

 

[BBAI BBAI]

See, if you have solved the sum of electric flux( i.e flux through one face of a cube containing a charge Q inside it.=Q/6e0) you can understand.The similar follows here...Instead of Surface integral here is the line integral..

 

[ehild]

Solve it by using Faraday's Low of Induction

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/maxeq2.html#c3.

The electric field lines are circles around the cylinder. The line integral for a whole circle is equal to the negative of the derivative of magnetic flux inside. It does not depend on the actual path. You can use symmetry to calculate the integral for the given path.

ehild

 

[Saitama]

Solve it by using Faraday's Low of Induction

http://hyperphysics.phy-astr.gsu.edu/hbase/electric/maxeq2.html#c3.

I did use the integral form to get the magnitude of electric field.

The electric field lines are circles around the cylinder. The line integral for a whole circle is equal to the negative of the derivative of magnetic flux inside. It does not depend on the actual path. You can use symmetry to calculate the integral for the given path.

ehild

I am not sure if I get it but what about the case when the square shown in attachment 3 lies inside the circle $x^2+y^2=a^2$? Would the same method still apply?

Thanks!

 

[ehild]

The enclosed flux counts.

ehild

 

[Saitama]

The enclosed flux counts.

ehild

For instance if I inscribe a square of side a/√2 in the given circular region, the line integral for that square would be $\frac{d\phi}{dt}$ where $\phi=(B_0t)(a^2/2)$. Is this correct?

Thanks!

 

[ehild]

Yes.

 

[Saitama]

Yes.

Thanks a lot ehild!