- #1
Jtechguy21
- 51
- 0
Homework Statement
Hello, this is my first time taking physics in college, and I have read the section twice and I this is what I understand. If someone could point me in the right direction, that would be great.
For example:
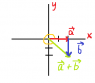
How do I find the angle for example from Vector a + Vector b.
Would I use the tail to head method and that would give me a reference angle of 90 degrees, and rank accordingly? Or am i missing something here
Homework Equations
hint1)
The vector resulting from the combination a⃗ +b⃗ is the only vector that lies outside of the first quadrant. The first quadrant is the portion of the xy coordinate axes that lies between the positive x-axis and the positive y axis.
hint2)
You may add the vectors either geometrically or by determining the components of the vectors and adding component-wise. Once you have done the necessary vector additions, you can measure the angles from the positive x-axis counterclockwise to the resultant vectors.
 )
)