Vector Proof Homework: Show Invariance of Distance from Origin

[uchicago2012]

Homework Statement

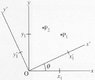
An (x,y) coordinate system is rotated through an angle theta to produce an (x',y') system, see figure.
A point with coordinates (x,y) will have coordinates (x',y') in the rotated system given by:
x'₁ = (x₁ * cos theta) + (y₁ * sin theta)
y'₁ = (-x₁ * sin theta) + (y₁ * cos theta)
Show that the formula for the distance of the point from the origin is invariant, or unchanged, by the rotation. That is, show:
sqrt (x₁² + y₁²) = sqrt (x'₁² + y'₁²)

Homework Equations

I don't know if these are really relevant, I just thought so:
a_x = a cos theta
a_y = a sin theta
a = sqrt (a_x² + a_y²)
tan theta = a_y/a_x
where a = the magnitude of vector a and theta = the angle vector a makes with the positive direction of the x axis

The Attempt at a Solution

So I thought this was asking, more or less, to prove that rotating the axes changes the components of the vector but not the vector itself.

I set the two equations given equal to each other, subbing in the information given for x' and y', but I don't know how to proceed or even if this was a good place to start. Any ideas for starting off?

sqrt (x₁² + y₁²) = sqrt (((x₁ * cos theta) + (y₁ * sin theta))² + ((-x₁ * sin theta) + (y₁ * cos theta))²)

 

[collinsmark]

So I thought this was asking, more or less, to prove that rotating the axes changes the components of the vector but not the vector itself.

I set the two equations given equal to each other, subbing in the information given for x' and y', but I don't know how to proceed or even if this was a good place to start. Any ideas for starting off?

sqrt (x₁² + y₁²) = sqrt (((x₁ * cos theta) + (y₁ * sin theta))² + ((-x₁ * sin theta) + (y₁ * cos theta))²)

'Looks good to me so far.

Leave the left side of the equation alone. Start expanding the right side. See if any terms cancel out as you go. Eventually you will find the trig identity,

$$\cos^2 \theta + \sin^2 \theta = 1$$

quite useful.

 

[uchicago2012]

So I worked on the given equation, simplifying until I got:

(x₁² + y₁²)^1/2 = ( (x₁ * cos theta)² + (x₁ sin theta)² + 4(x₁ * cos theta * y₁ * sin theta) + (y₁ * sin theta)² + (y₁ * cos theta)² )^1/2

But I don't see where to go from here. I feel as if I should be able to see a² + b² (as in the Pythagorean theorem) in this mess, but I don't see it. Perhaps that's just off base anyway and I just haven't done enough algebra.

 

[collinsmark]

So I worked on the given equation, simplifying until I got:

(x₁² + y₁²)^1/2 = ( (x₁ * cos theta)² + (x₁ sin theta)² + 4(x₁ * cos theta * y₁ * sin theta) + (y₁ * sin theta)² + (y₁ * cos theta)² )^1/2

But I don't see where to go from here. I feel as if I should be able to see a² + b² (as in the Pythagorean theorem) in this mess, but I don't see it. Perhaps that's just off base anyway and I just haven't done enough algebra.

The term in red involves a little mistake. But that little mistake makes a big difference.

Here's a hint. In your original substitution,

$$\sqrt{\left( x_1 \cos \theta + y_1 \sin \theta \right) ^2 + \left( {\color{red}{-}} x_1 \sin \theta + y_1 \cos \theta \right) ^2},$$

the x₁sinθ has a negative sign attached to it (in red, directly above). However, when you expanded all the terms, everything somehow ended up positive (which is where the mistake fits in).