Velocity of Center of Mass of Disk

[Tanya Sharma]

Homework Statement

Homework Equations

The Attempt at a Solution

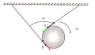
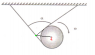
I think if I can locate the instantaneous axis of rotation ,then may be motion/velocity of CM could be determined . In the attached figure I have marked the two points A and B which are instantaneously at rest .The black arrows depict their respective velocities w.r.t CM .

Now consider point A . If it is instantaneously at rest ,then $V_{CM}$ has to be along the green vector .Similarly If we consider point B , then $V_{CM}$ should be along the red vector .

But that is a contradiction . I am not very sure if this is the right way to approach this problem .

I would be grateful if somebody could help me with the problem .

 

[TSny]

Locating the instantaneous axis of rotation sounds like a very good idea!

Are the points A and B instantaneously at rest? Hint: Are the strings changing their angles with respect to the vertical?

 

[Tanya Sharma]

Are the points A and B instantaneously at rest? Hint: Are the strings changing their angles with respect to the vertical?

Yes . I have been thinking on this line . No , the points are not at rest . I am guessing that the left string is rotating clockwise whereas right is rotating anticlockwise w.r.t the support . Is that correct ?

So what should be the next line of thinking ?

 

[TSny]

Yes . I have been thinking on this line . No , the points are not at rest . I am guessing that the left string is rotating clockwise whereas right is rotating anticlockwise w.r.t the support . Is that correct ?

Yes.

So what should be the next line of thinking ?

Can you see the direction that point A (on the disc) must be moving?

 

[Tanya Sharma]

Before I answer your question , I would like to clarify ,whether it is correct to say that point A is instantaneously at rest w.r.t the string ?

 

[TSny]

Before I answer your question , I would like to clarify ,whether it is correct to say that point A is instantaneously at rest w.r.t the string ?

Yes. It is like a ball rolling without slipping on a board that is being tilted.

 

[Tanya Sharma]

Fine .

Are you getting $V_{CM} = \frac{\omega R}{cos\frac{\alpha}{2}}$

In the attached figure ,the green dot represents the IAOR and red vector represents the direction of velocity of CM .

Does that make sense ?

 

[TSny]

I believe your answer is correct.

 

[Tanya Sharma]

Did you have a look at the attached figure as well ?

 

[TSny]

Did you have a look at the attached figure as well ?

Yes, it looks good to me. Something to think about: does the answer make sense for $\alpha$ approaching zero?

 

[Tanya Sharma]

Yes, it looks good to me.

Thank you very much

Something to think about: does the answer make sense for $\alpha$ approaching zero?

Yes ,it makes sense. I am assuming this situation corresponds to when the two strings are aligned one on top of the other vertically (i.e both the strings are vertical) . In this case $V_{CM} = \omega R$

Do you see any issue ?

 

[Tanya Sharma]

A side question -

If a disk is rolling without slipping(accelerated/non-accelerated) on a stationary horizontal surface ,the bottommost point is at rest . Is it correct to say that this point does not have any kind of acceleration , neither linear nor centripetal acceleration ? I am concerned more about centripetal acceleration .

 

[TSny]

Thank you very much
Yes ,it makes sense. I am assuming this situation corresponds to when the two strings are aligned one on top of the other vertically (i.e both the strings are vertical) . In this case $V_{CM} = \omega R$

Do you see any issue ?

I think it makes sense, as you say. You can also think about $\alpha$ going to 180^o, with the two strings horizontal.

 

[TSny]

A side question -

If a disk is rolling without slipping(accelerated/non-accelerated) on a stationary horizontal surface ,the bottommost point is at rest . Is it correct to say that this point does not have any kind of acceleration , neither linear nor centripetal acceleration ? I am concerned more about centripetal acceleration .

The point will have a centripetal acceleration (i.e., upward) at the instant the point is at rest.

 

[Tanya Sharma]

The point will have a centripetal acceleration (i.e., upward) at the instant the point is at rest.

The point is at rest i.e v=0 .Shouldn't the centripetal acc. v²/R be zero as well? Please explain this apparent contradiction .

 

[TSny]

Look at the motion https://en.wikipedia.org/wiki/Cycloid. Is the vertical component of velocity changing when the point is in contact with the surface?

What if you switch to the inertial reference frame moving with the center of the disk? In this frame would the point have a vertical component of acceleration at the lowest position? Do accelerations change when switching between inertial reference frames?

 

[Tanya Sharma]

Okay .

There is another problem involving similar concepts of rolling and use of Instantaneous axis . Please see the attached picture .

Do you agree that in the inertial frame moving with the center of the sphere

1) speed of the lower tip is 'v' towards left .
2) speed of the topmost point is 'v' vertically upwards .
3 rod is undergoing pure rotation about the center of the sphere .
4) the center of the sphere acts as the instantaneous axis .
5) the CM of the rod is moving with speed v/√2 .

 

[TSny]

I agree with all 5.