- #1
- 2,810
- 604
I'm reading these lecture notes but there is something I don't understand. In page 15, it starts to consider vacuum diagrams of various orders and tries to associated a factor to them according to the rule:
## diagram \sim (\frac \lambda N)^p(\frac N \lambda)^v N^l=\lambda^{p-v} N^{l+v-p}##.
Where v is the number of vertices, p is the number of propagators and l is the number of loops.
But I have some problems with understanding a few of its countings.
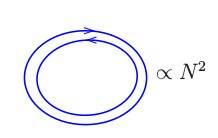
In this one, I think, you can consider any number of vertices you want and it doesn't matter because the number of propagators will be equal to it and they will cancel each other. But what does matter is the number of loops which, for me, is obviously equal to 1. But as you can see, the papers says its 2 and I have no idea how!
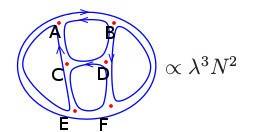
In this one, there are 6 vertices and 9 propagators. The factor that the paper assigns to it suggests that the number of loops should be 5. So let's count! I start from A:
AECA,AECDBA, AEFDCA, AEFDBA, AEFBA, AEFBDCA,...
I think there are still more A-containing loops but it doesn't matter. There are already 6 loops and I didn't even go to loops containing other vertices(like CDFEC). So how does the paper say the number of loops is 5?
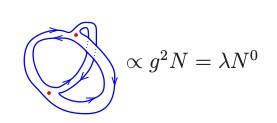
This one has 2 vertices and 3 propagators and so the number of loops should be 1, according to the factor given to it by the paper. But I see 3 loops! Let's call the top vertex F and the bottom one G. If I'm on each of the vertices, then I have three directions to go, let's call them east,west and north. So let's say I'm on F. Then I can go to north to reach G. Then I can either go to west or east to return to F. So we have 2 loops here. Another loop is going east(west) to reach G and then going west(east) to return to F. So there are 3 loops in this diagram, but the paper says its 1. How?
Thanks
## diagram \sim (\frac \lambda N)^p(\frac N \lambda)^v N^l=\lambda^{p-v} N^{l+v-p}##.
Where v is the number of vertices, p is the number of propagators and l is the number of loops.
But I have some problems with understanding a few of its countings.
In this one, I think, you can consider any number of vertices you want and it doesn't matter because the number of propagators will be equal to it and they will cancel each other. But what does matter is the number of loops which, for me, is obviously equal to 1. But as you can see, the papers says its 2 and I have no idea how!
In this one, there are 6 vertices and 9 propagators. The factor that the paper assigns to it suggests that the number of loops should be 5. So let's count! I start from A:
AECA,AECDBA, AEFDCA, AEFDBA, AEFBA, AEFBDCA,...
I think there are still more A-containing loops but it doesn't matter. There are already 6 loops and I didn't even go to loops containing other vertices(like CDFEC). So how does the paper say the number of loops is 5?
This one has 2 vertices and 3 propagators and so the number of loops should be 1, according to the factor given to it by the paper. But I see 3 loops! Let's call the top vertex F and the bottom one G. If I'm on each of the vertices, then I have three directions to go, let's call them east,west and north. So let's say I'm on F. Then I can go to north to reach G. Then I can either go to west or east to return to F. So we have 2 loops here. Another loop is going east(west) to reach G and then going west(east) to return to F. So there are 3 loops in this diagram, but the paper says its 1. How?
Thanks