Very Simple Work/Energy Pendulum Problem

[Bread Boy]

Homework Statement

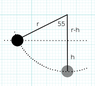
A 2.0kg bob of a pendulum is held at an angle of 55 degrees from the vertical. When released it reaches a maximum speed of 3.5m/s. What is the length of the pendulum arm?

Homework Equations

Ek = 1/2mv^2
Ep = mgh

The Attempt at a Solution

1/2 * 2 * 3.5 ^ 2 = 12.25 J
12.25 = 2(9.8)h
h = 0.625

That's as far as I can get. I know that the length of the pendulum arm is 0.625 plus "length - 0.625" but I'm stuck there. Help would be much appreciated :)

Thanks in advance!

 

[Simon Bridge]

Draw the picture - h is the vertical distance between the start position and the bottom of the arc - and you know the angle of the arc is 55 degrees.

Construct the obvious triangle and use trig.

 

[Bread Boy]

Could you please specify what the triangle would look like and which trig functions to use? I know that h is the vertical distance between the start position and the bottom of the arc and that I should use trig on a constructed triangle but I'm a little brain dead as of now and totally stonewalled.

 

[Simon Bridge]

Did you draw the picture?
There's only like, two possible triangles.

Hint: you want the one where the third side is horizontal.
Draw it and stare at it - keep staring at it: what is the length of the hypotenuse? What is the length of the vertical side? How are these related?

 

[Bread Boy]

I did draw the picture; there's a big triangle of which the three sides are the vertical, the string, and an imaginary horizontal line, and a small one of which the three sides are h, the imaginary horizontal, and a hypotenuse roughly where the pendulum bob would swing. I've been staring at it for a good half hour before making a topic... maybe my algebra or trig is rusty? Sorry Simon, I'm not seeing anything.

 

[Simon Bridge]

You will kick yourself...

Write the expression for the cosine of 55 using this triangle, and solve for r.

 

[Bread Boy]

Thanks for the diagram! That's what I had down, and I tried to use sine law but I can only get to sin35 = (r - 0.625) / r

I hate having people spell things out for me but I am just not getting this :(

 

[Simon Bridge]

That should do it! You just used the complimentary angle.
I was suggesting you do:$$\cos(55)=\frac{r-h}{r}$$(remember SOH CAH TOA?)
But yours is exactly the same.

Now solve for r.

You can do algebra right?
This is an equation of the form: ax = x - b