person123
- 326
- 52
I'm a bit confused about the viscosity term in the Navier-Stokes equation; my intuitive understanding of what it would is different from what it actually is.
I took the z component of the stress on an infinitesimal cube, but the same approach should apply in the x and y direction. I think my method might be a bit sloppy (maybe leading to the error), but I'm not sure how to be more precise. I end up missing the third term of the Laplacian, the second derivative of the z component of velocity with respect to z. What am I missing?
Thanks.
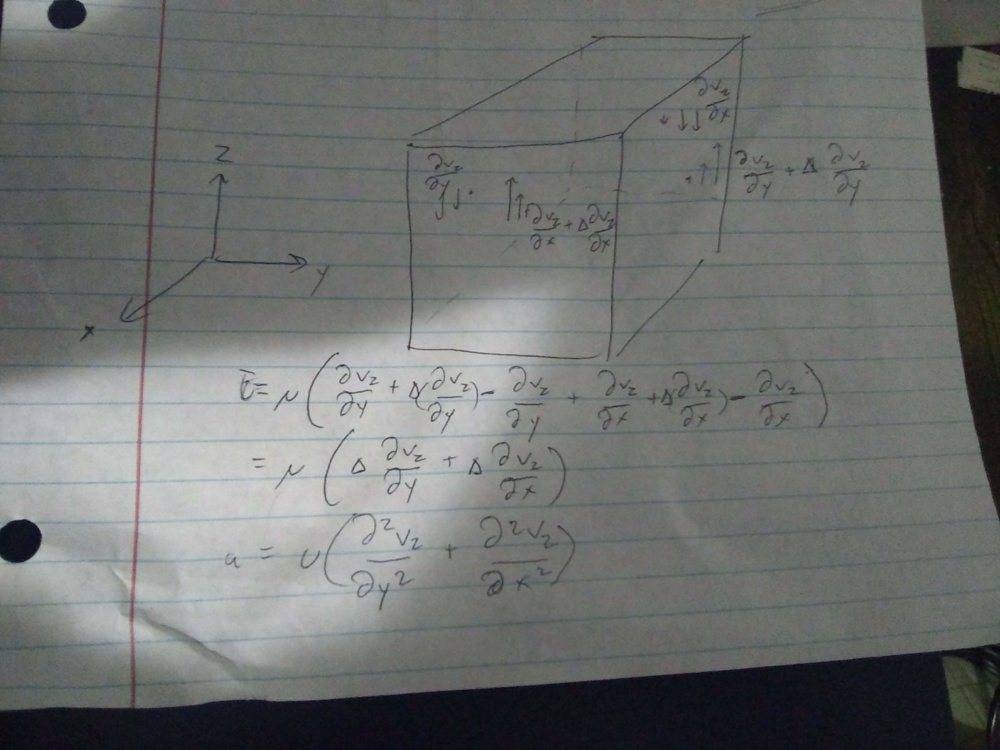
I took the z component of the stress on an infinitesimal cube, but the same approach should apply in the x and y direction. I think my method might be a bit sloppy (maybe leading to the error), but I'm not sure how to be more precise. I end up missing the third term of the Laplacian, the second derivative of the z component of velocity with respect to z. What am I missing?
Thanks.
