Engineering Voltage and phase between two branches of ac circuit

[Tom Moynihab]

_【Mod Note: moved from technical forum, so homework template is missing_】

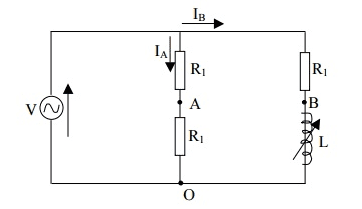
In a parallel circuit, one branch contains two equal resistors of resistance $R_1$ connected in series. The other branch contains a resistor of resistance $R_1$ in series with an inductor of variable inductance $L$.
Show that the magnitude $|V_{AB}|=\frac{V}{2}$ and $\phi=\tan^{-1}\big(-\frac{2\omega LR_1}{R_1^2-\omega^2L^2}\big)$https://gyazo.com/50cbf5ef913b0fc533ebcb0074b3b5a3 (Very sorry for the link, but the image uploader wasn't working for me)

{image inserted by moderator}I have worked out that total impedance =$|Z|=\frac{2R_1(R_1+\omega L)}{3R_1+\omega L}$ Which I'm not sure is correct.

I'm thinking that I have to work out what fraction of voltage $R_1$ gets in the $B$ branch, but I'm pretty confused.

Edit: I have managed to prove $|V_{AB}|=\frac{V}{2}$ and am now stuck on the second part, it's only two marks so it shouldn't be difficult, I just don't know what impedance I'm meant to be taking

Any help on this would be really appreciated :)

 

[NascentOxygen]

Hi Tom Moynihab.

You need to enclose your Latex inside double hash marks, not single dollars. You can use double dollars where you want it presented on a new line.

 

[Tom Moynihab]

You need to enclose your Latex inside double hash marks, not single dollars.

oh sorry, which tex plugin is used?

 

[NascentOxygen]

MathJax does its work at the server and it is sent to you as javascript, I think.

 

[Tom Moynihab]

MathJax does its work at the server and it is sent to you as javascript, I think.

oh hmm I'm not getting any tex, still all code. Also is this visible/what do i need to do to make it visible?

 

[NascentOxygen]

oh hmm I'm not getting any tex, still all code. Also is this visible/what do i need to do to make it visible?

If you are using the PF app it displays the raw MathJax code. You'll need to use a browser to see your LaTex creation in its full glory.

 

[Tom Moynihab]

If you are using the PF app it displays the raw MathJax code. You'll need to use a browser to see your LaTex creation in its full glory.

I am currently using chrome though. Edit: fixed it, had to turn off my previous plugin

 

[Tom Moynihab]

If you are using the PF app it displays the raw MathJax code. You'll need to use a browser to see your LaTex creation in its full glory.

Sorry my post currently visible?

 

[gneill]

Edit: I have managed to prove $|V_{AB}|=\frac{V}{2}$ and am now stuck on the second part, it's only two marks so it shouldn't be difficult, I just don't know what impedance I'm meant to be taking

For the phase angle, you've probably done most of the work already when proving that $|V_{AB}|=\frac{V}{2}$. Can you show that work up to the point where you found the magnitude?

 

[Tom Moynihab]

For the phase angle, you've probably done most of the work already when proving that $|V_{AB}|=\frac{V}{2}$. Can you show that work up to the point where you found the magnitude?

Well it might be a bit of a jump, but I said for A it was V/2 as the voltage simply splits 50/50. Then for B I said as the impedance between the resistor and the inductor is pi/2 out of phase, therefore voltage across the resistor varies between V and 0... and I just called it 0.

 

[gneill]

Well it might be a bit of a jump, but I said for A it was V/2 as the voltage simply splits 50/50. Then for B I said as the impedance between the resistor and the inductor is pi/2 out of phase, therefore voltage across the resistor varies between V and 0... and I just called it 0.

I'm afraid that doesn't hold water as a derivation. You'll need to return to that part and do the math.

The A branch is a simple voltage divider as you pointed out. But so is the B branch. The only difference is that one of the elements is an inductor rather than another resistor. You should be able write an expression for the potential at point B using the voltage divider formula.

 

[Tom Moynihab]

I'm afraid that doesn't hold water as a derivation. You'll need to return to that part and do the math.

The A branch is a simple voltage divider as you pointed out. But so is the B branch. The only difference is that one of the elements is an inductor rather than another resistor. You should be able write an expression for the potential at point B using the voltage divider formula.

The part which confused me was that the voltage from A is already V/2, therefore B has to be 0, which means surely the circuit wouldn't work?

 

[cnh1995]

The part which confused me was that the voltage from A is already V/2, therefore B has to be 0, which means surely the circuit wouldn't work?

That's not correct. Branch B contains an inductor. You need to consider the phase difference between voltages at A and B.

 

[gneill]

Following on to what @cnh1995 said, if you do the algebra you'll find the answers to both the voltage magnitude and the phase angle questions.

 

[Tom Moynihab]

That's not correct. Branch B contains an inductor. You need to consider the phase difference between voltages at A and B.

So as the impedance for a resistor is just R and the impedance for an inductor is [;j\omega L;] meaning they are [;\frac{\pi}{2};] out of phase with each other, meaning that when [;V_R=R*0;] and [;V_L=X_L*I_{max};] maybe? Am I at least on the right track? I am going to bed now as it is 3.30AM, but I will check tomorrow

 

[gneill]

Do the math; it's just a bit of complex algebra. It'll automatically take care of the phase relationships without your having to make guesses. Certainly when the circuits get more complicated you won't be able to use handwavy arguments to analyze them.

 

[Tom Moynihab]

Following on to what @cnh1995 said, if you do the algebra you'll find the answers to both the voltage magnitude and the phase angle questions.

Do the math; it's just a bit of complex algebra. It'll automatically take care of the phase relationships without your having to make guesses. Certainly when the circuits get more complicated you won't be able to use handwavy arguments to analyze them.

I think my problem is setting up the correct math, it's confusing to me what to do, could you help with that please?

 

[gneill]

Look up: "voltage divider" (or "potential divider").

 

[cnh1995]

I think my problem is setting up the correct math, it's confusing to me what to do, could you help with that please?

I think my problem is setting up the correct math, it's confusing to me what to do, could you help with that please?

Would you be comfortable with the phasor approach?

 

[Tom Moynihab]

Would you be comfortable with the phasor approach?

Yeah I am, many thanks

 

[cnh1995]

Yeah I am, many thanks

Ok.
Can you develop the phasor diagram?
Take the inductor voltage as reference phasor.

 

[cnh1995]

Ok.
Can you develop the phasor diagram?
Take the inductor voltage as reference phasor.

I think taking supply voltage as reference phasor would be the right approach.

 

[NascentOxygen]

So as the impedance for a resistor is just R and the impedance for an inductor is [;j\omega L;] meaning they are [;\frac{\pi}{2};] out of phase with each other, meaning that when [;V_R=R*0;] and

This is not valid for inline LaTex here. PF MathJax needs to be enclosed between double hash symbols, e.g. $[/color]j\omega L$[/color]