Voltage drop conceptual questions

[PhysicsInNJ]

I'm having trouble understanding how voltage drops.

My understanding of voltage is a difference in potential, with potential being how much work is necessary to move a test charge to a specific orientation.
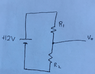
So, if we have a circuit with say, a 12V battery and a 1 ohm resistor, and I had a +1 coulomb charge sitting at the negative terminal I would have to apply 12 joules of work to move it to the positive terminal.
My confusion begins here: why, If I do this in real life, no matter where I take check the potential difference with a voltmeter I always will get 12V whether from the negative terminal or, after the resistor.

Is it because the wire/resistor have charge carriers and essentially become "terminals" wherever I decide to place my voltmeter?

Then, when considering a simple voltage divider with two resistors of equal value, what happens to the other half of the potential? Shouldn't it require the same amount of work to bring that test charge to the positive terminal?

 

[Dale]

Is it because the wire/resistor have charge carriers and essentially become "terminals" wherever I decide to place my voltmeter?

Basically, yes. The purpose of the wire is to make sure that the negative terminal and the end of the resistor are at the same potential, so we would be surprised if it weren’t true.

Then, when considering a simple voltage divider with two resistors of equal value, what happens to the other half of the potential?

If you have a voltage divider with two equal resistors, R, and a voltage source, V, then the voltage across each resistor will be V/2 independent of R.

 

[jartsa]

If we multiply the current that is going through a resistor by the resistance of said resistor, we get the voltage over the resistor. We often say that voltage over a battery is the voltage of the battery, so let's say the voltage over the resistor is the voltage of the resistor.

And now we draw a picture of a circuit consisting of a battery and a resistor, and the voltages of those components. I will not bother with any numbers, just the directions of the voltages will suffice for our purposes.

A circuit with a resistor and a battery looks like this: (R is resistor, B is battery, the wire that completes the circuit is not drawn)

--------_-R₊---₊B_-------------And a circuit with two resistors and two batteries looks like this:

--------_-R₊---_-R₊-----------₊B_----₊B_-------------So now we take a voltmeter and stick the electrodes to various points of that above circuit - what voltages do we measure?

 

[jbriggs444]

If we multiply the current that is going through a resistor by the resistance of said resistor, we get the voltage over the resistor. We often say that voltage over a battery is the voltage of the battery, so let's say the voltage over the resistor is the voltage of the resistor.

And now we draw a picture of a circuit consisting of a battery and a resistor, and the voltages of those components. I will not bother with any numbers, just the directions of the voltages will suffice for our purposes.

A circuit with a resistor and a battery looks like this: (R is resistor, B is battery, the wire that completes the circuit is not drawn)

--------_-R₊---₊B_-------------And a circuit with two resistors and two batteries looks like this:

--------_-R₊---_-R₊-----------₊B_----₊B_-------------So now we take a voltmeter and stick the electrodes to various points of that above circuit - what voltages do we measure?

If we denote the resistance of resistor R by R and the voltage of battery B by V then we can deduce that the current flowing in the circuit must be $\frac{2V}{2R} = \frac{V}{R}$
The voltage rise across each battery is V. The voltage drop across each resistor is V. The measured potential difference between any two distinct terminals in the circuit is accordingly +V, +2V, -V or -2V and will depend on where the two probes from the voltmeter are placed.

 

[PhysicsInNJ]

Basically, yes. The purpose of the wire is to make sure that the negative terminal and the end of the resistor are at the same potential, so we would be surprised if it weren’t true.

If you have a voltage divider with two equal resistors, R, and a voltage source, V, then the voltage across each resistor will be V/2 independent of R.

If we denote the resistance of resistor R by R and the voltage of battery B by V then we can deduce that the current flowing in the circuit must be $\frac{2V}{2R} = \frac{V}{R}$
The voltage rise across each battery is V. The voltage drop across each resistor is V. The measured potential difference between any two distinct terminals in the circuit is accordingly +V, +2V, -V or -2V and will depend on where the two probes from the voltmeter are placed.

So really my question becomes the following: In voltage divider like the one below, where R1=R2, When I check Vout it will be 6V. If i had 1 resistor, the voltage would be 12V. How is the addition of a second resistor changing the voltage? Worded longer, if potential is how much work is needed to move a test charge, that should remain the same for moving a test charge from R1 to the terminal, regardless of the addition of another resistor.

 

[ZapperZ]

So really my question becomes the following: In voltage divider like the one below, where R1=R2, When I check Vout it will be 6V. If i had 1 resistor, the voltage would be 12V. How is the addition of a second resistor changing the voltage? Worded longer, if potential is how much work is needed to move a test charge, that should remain the same for moving a test charge from R1 to the terminal, regardless of the addition of another resistor.

But the work done depends on the change in potential, not the value of the resistance. So why do you expect the work done by a charge moving across R1 to be the same no matter what the potential is?

Try it this way. Use ONLY R1, but then vary the source potential. You are claiming that no matter what potential I put across R1, the work done in a charge moving across R1 is the same. This is clearly not correct.

Zz.

 

[jbriggs444]

When I check Vout it will be 6V.

When you check vout against what? You cannot measure voltage with only one lead to your voltmeter. Where is the other lead on the voltmeter attached?

 

[jartsa]

----------BATTERY_A--------------------_BRESISTOR--_C-----It takes no energy at all to move a charge from B to A. Why? Well because the charge is repelled by one end of the battery, and the charge is repelled by one end of the resistor. Net effect is zero.

It takes energy to move a charge from C to B. The C-end of the resistor attracts the charge, the B-end of the resistor repels the charge.

And It takes energy to move a charge from C to A. The C-end of the resistor attracts the charge, the A-end of the battery repels the charge.

We move the charge over the resistor, not through it. That's the easiest way to think about it.

My point is that the accumulated charges on the two ends of the resistor are a cause of a potential difference, or a voltage.

 

[Dale]

How is the addition of a second resistor changing the voltage?

It’s a completely different circuit. I don’t think it makes sense to compare those two voltages and ask how one changes to the other. The node where the 6 V is measured does not even exist in the single resistor circuit. So there is no obvious sense in which one voltage changes into the other.

You have two different circuits. In one circuit one voltage is 12 V and in another circuit a completely different voltage is 6 V.

 

[Joshy]

Maybe the confusion is due to the reference? In your brief analysis: Your reference "ground" is the negative terminal of the voltage supply. You could really move your reference wherever you'd like. The voltages with respect to that reference may change, but the voltage across individual components such as a single resistor will remain the same.

You see? The voltage across each resistor is still 6 V and the voltage across the supply goes from -6 V to 6 V with respect to the ground; this is still 12 V across the supply although it isn't from 0 V to 12 V like the first example.

So: When you take the voltmeter and touch one probe to one node and the other probe to another, then one of those probes acts like the reference (ground) with respect to whatever you're measuring using its counterpart. If you take the two probes and touch the same node/wire in any part of the DC circuitry, then the voltage across it will look like 0 V.

 

[Drakkith]

So really my question becomes the following: In voltage divider like the one below, where R1=R2, When I check Vout it will be 6V. If i had 1 resistor, the voltage would be 12V. How is the addition of a second resistor changing the voltage?

To use the water analogy, imagine the current through the circuit like water through pipes, with the resistors representing long and narrow pipes and wires representing short, fat pipes. Water moving through the short pipes loses little energy through friction since the pipes are short and fat. However the water loses much more of its energy as it moves through the long and narrow pipes. If we connect Vout to the water circuit right before the water gets to R1, then we have lots and lots of potential energy available since the water hasn't lost most of its energy yet. If Vout was also a short, fat pipe, then the current would rush through Vout at a very high flow rate, much higher than what would go through R1, to get back to the pump, and little would go through R1. This is analogous to how shorting the terminals of R1 would lead to a short circuit, with most of the current moving through the short and little moving through R1. If we instead have Vout as a tube that is even longer and narrower than R1, we get an analogous situation to a voltmeter, which has a very high resistance compared to the circuit being measured.

Connecting Vout below R1 will show us that most of the water's potential energy has been expended passing through R1. Connecting a short, fat pipe between the exit of R1 and the pump does almost nothing. The water just doesn't have any extra energy left. It's like connecting an additional wire between one terminal of R1 and the voltage source. You'll split the current flowing through the wire, but the circuit won't change other than that.

If we add R2 so that Vout is now between R1 and R2, and keep R1=R2, then half of the water's potential energy is expended passing through R1 before it ever comes to R2 or Vout. Note here that the resistance felt by the water passing through R2 is transferred to the rest of the circuit through the water. That's how the water passing through R1 'knows' how much energy to expend. It's experiencing a force from the sides of R1 as friction and an additional force from the water in R2. Since the initial pressure hasn't changed, in order to conserve energy the current has to slow down.

Worded longer, if potential is how much work is needed to move a test charge, that should remain the same for moving a test charge from R1 to the terminal, regardless of the addition of another resistor.

That's right, but remember that you're not moving a single test charge from R1 to the terminal, you're moving a trillion trillion quintillion charges throughout the entire circuit all at once. Whatever energy is being expended is split between the charges throughout the circuit in a continuous process as time passes. This is a case where simplifying things down to a single particle probably confuses you more than it helps you. The fact is that an electric circuit is not composed of single charges moving by themselves along the circuit, they are composed of enormous numbers of charges that all interact with each other and the EM field.

Defining electric potential in terms of a test charge is useful for understanding a very simple example, but the real world is never that simple.