theno1katzman
- 21
- 0
Homework Statement
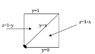
Find exactly the volume in the first octant under the planes x + z =1 and y + z =1. Find the mass if the density is p(x,y,z)=xyz.
The Attempt at a Solution
This is a pyramid in shape, so for the volume, rather than constructing a double integral, I used the formula V= Bh/3 which is equal to 1/3.
Please see the jpg file for the work on finding the mass.
Where did I go wrong? It came out to be 0.
I tried reversing the z limits and that didn't do anything.