Wedges problem -- When will the two wedges start sliding?

[mingyz0403]

Homework Statement

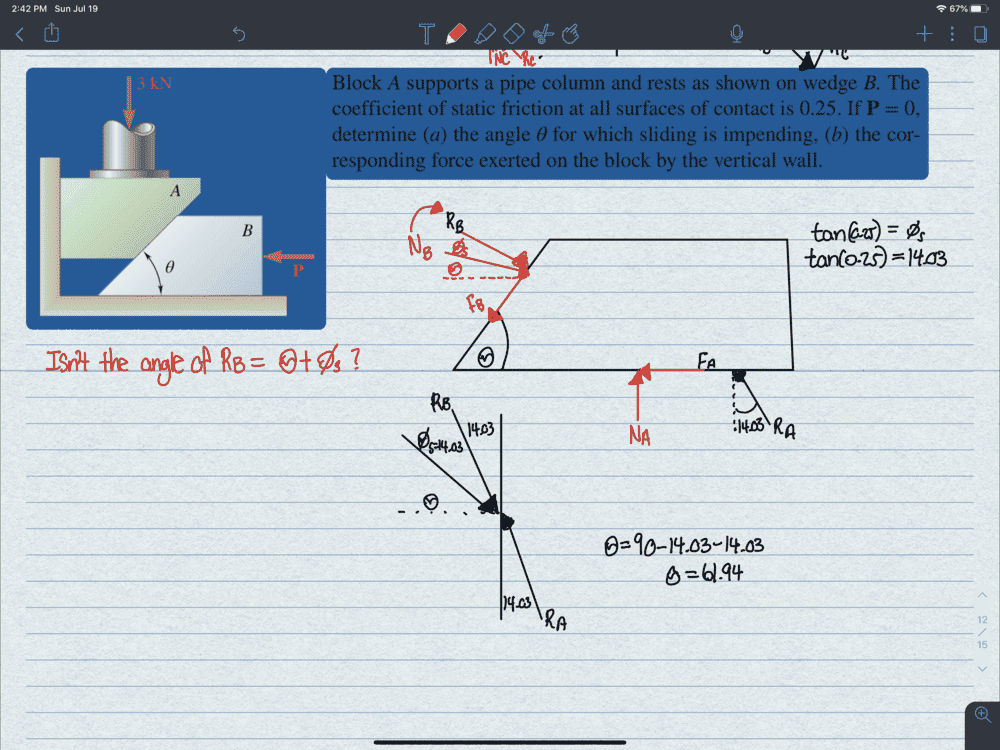
Block A supports a pipe column and rests as shown on wedge B. the coefficient of static friction at all surfaces of contact is 0.25. if p = 0, determine (a) the angle θ for which sliding is impending, (b) the corresponding force exerted on the block by the vertical wall.

Relevant Equations

Free body diagram

The correct angle is 28.1 degree.I understand ∅=arctan(m). Isn’t R should be angled ∅ degree away from the normal force.

 

[Charles Link]

I have what I presently would call a somewhat sloppy solution that gets the correct answer to the angle.

If you just look at the wedge B, and consider it massless, you can assume a normal force $F_N$ acts on it from the block. The downward forces on the wedge consist of the vertical component of $F_N$, along with a downward component of the frictional force between the block and the wedge. These create a horizontal frictional force at the base, that balance the combination of the horizontal component of the normal force (pushing to the right) and the horizontal component of the frictional force on the wedge from the block (which points to the left=thereby a minus sign).

The $F_N$ drops out from both sides of this expression, and you solve for $\tan{\theta}=\sin{\theta}/\cos{\theta}$. I'll be glad to supply additional detail on this expression if you get stuck, but you should be able to write out the expression from the info I provided.

 

[Charles Link]

To add to the above, and make the solution of the problem a little more complete, it may really be better to exclude gravity (and masses of the wedge and block) in this problem=e.g. letting the system be on a horizontal frictionless table. In this case it is clear that the mass B can be ignored, as was done to get the answer given by the textbook.

 

[Charles Link]

We haven't heard back from the OP on this one, but I'd like to add something that the OP and anyone else may find of interest:
*
The frictional force reaches its maximum value $F_F =\mu F_N$ when motion is imminent, and is opposite the direction of motion. Otherwise, the frictional force can even be zero with a large normal force=e.g. a book resting on a horizontal table has zero frictional force unless there is an applied force that attempts to move the book. The frictional force will then be opposite the applied force, and its maximum value is $F_F=\mu F_N$. $\\$
*
With this additional input, the "algebraic" solution I came up with above becomes more complete.