- #1
berdan
- 32
- 0
Hi,
So,I'm helping a guy with his mechanical engineering homework.
The problem is that the guy is so off, he doesn't even know the name of the subject.
And honestly, I having a hard question finding out what this question is about.
I need to proove the Zb=h^2/3 thingy. I have no idea what this is about.
Can someone point me to the subject?
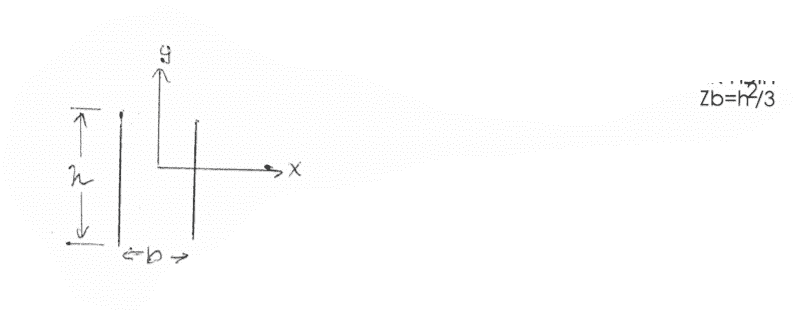
So,I'm helping a guy with his mechanical engineering homework.
The problem is that the guy is so off, he doesn't even know the name of the subject.
And honestly, I having a hard question finding out what this question is about.
I need to proove the Zb=h^2/3 thingy. I have no idea what this is about.
Can someone point me to the subject?