TwoEG
- 13
- 0
While I was studying with electric field about cylinder, I learned that for a very long cylinder, the electric field in the hollow of cylinder will be zero.
http://physics.stackexchange.com/questions/156789/electric-field-of-hollow-cylinder
However, I couldn't accept this intuitively, and thought up this weird idea.
We can express electric field E of charged line like
##E=\frac \lambda {2\pi\epsilon_0 r}##
Thus, we knows that (+) charge between two parallel lines with same charge density will always move to their center, right?
Then, suppose we have a (+) charge in a cylinder other than on its axis, and let's see that cylinder above from it.
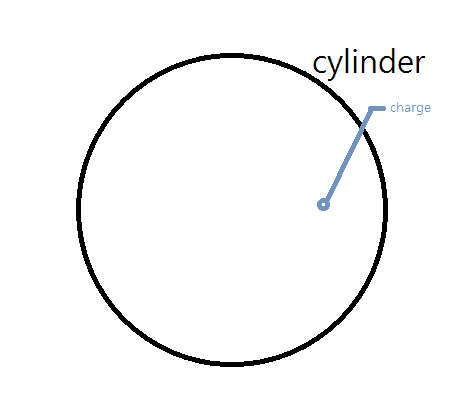
And this is what really confuses me.
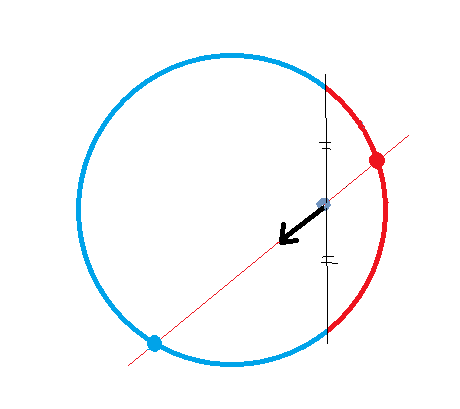
Draw a line that passes charge, then it'll meet with circle(cylinder) at two points(lines). Since a red dot(line) is always closer than a blue dot(line), sum of all forces will head to the left(?).
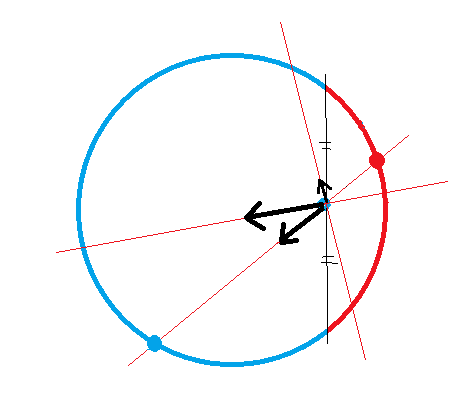
But this weird calculation conflicts with the fact that E=0 in the hollow of the cylinder.
What is a critical mistake of this logic(?). Will it be possible to explain why this image is wrong without using exact calculation?
http://physics.stackexchange.com/questions/156789/electric-field-of-hollow-cylinder
However, I couldn't accept this intuitively, and thought up this weird idea.
We can express electric field E of charged line like
##E=\frac \lambda {2\pi\epsilon_0 r}##
Thus, we knows that (+) charge between two parallel lines with same charge density will always move to their center, right?
Then, suppose we have a (+) charge in a cylinder other than on its axis, and let's see that cylinder above from it.
And this is what really confuses me.
Draw a line that passes charge, then it'll meet with circle(cylinder) at two points(lines). Since a red dot(line) is always closer than a blue dot(line), sum of all forces will head to the left(?).
But this weird calculation conflicts with the fact that E=0 in the hollow of the cylinder.
What is a critical mistake of this logic(?). Will it be possible to explain why this image is wrong without using exact calculation?