What are the conditions for a bench on an inclined plane to slide or tip?

[paalfis]

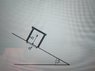
http://file://localhost/Users/pablotano_94/Downloads/IMG_20141205_183228102.jpg 1. Homework Statement
Assume that the friction coefficient (both static and dynamic) is ¨u¨.
a) What is the maximum slope yo can get in order that the bench does not slide?
b) What is the maximum slope yo can get in order that the bench does not turn?
c) What condition must be satisfied, while you are increasing the slope, in order that the bench turns but does not slide?

The Attempt at a Solution

My results where:
a)m*g*sin(B)<mgcos(B)*u
b)tan(B)<d/(2h)
c) u*m*g*cos(arctan(d/(2h))>m*g*sin(B)

This problem is supposed to be a tough one.. But my solution was quite simple, so, I think I am missing something, I really need some help with this one..
Thanks!

 

[Jazz]

I don't find the problem particularly tough, so I also suspect I'm missing something [:. But these were my thoughts related to your answers:

a) It's almost there, but if $mg\sin(\beta) = mg\cos(\beta)u$ I don't think the bench will slide.

b) and c) it's seems that you can solve them with one solution (that's the reason why I think I'm also missing something).

I assume the point at the top of the height h is the center mass. Think about the bench being on level ground and a person pushing in the upper left edge. There must be a force making it rotate around the lower right edge, and your equation for b) is not accounting for that. In what situation there will be equilibrium (there will be neither linear nor rotational net force)? What is causing the force (if there are any)? how is it related to the center of mass, h, and d?

 

[paalfis]

I had the same though, anyway, the question asks for the condition necessary for the bench to TURN (hopefully meaning turning all the way down) not for the conditions necessary for the rotation to start. That would be a very complicated problem, because you would need the acceleration for the rotation in order to see what it is needed to reach for the "critical" point of turning all the way.

 

[paalfis]

I think that the real problem comes when you consider that the normal force in each of the bench legs is different because of the angular momentum of the bench. Then, the front leg acts like a fulcrum and the rest of the bench turns with respect to it.
Sadly, I wasn't able to solve the problem this way..

 

[haruspex]

a)m*g*sin(B)<mgcos(B)*u

Right, but you can simplify that a lot. (Yes, it probably should include equality, but that's of no practical interest.)

c) u*m*g*cos(arctan(d/(2h))>m*g*sin(B)

I think it's looking for a condition that does not depend on beta. The slope will be gradually increased until it either slides or tips.

not for the conditions necessary for the rotation to start

No, it's only concerned with rotation starting. Once it starts it will continue until the bench has turned 90 degrees at least. You cannot tell what will happen after that since you do not know the full height of the bench.