What are the equations of these free fall/drag graphs?

[Dowon Kim]

Homework Statement

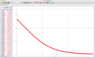
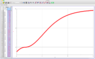
The screenshots of the graphs are attached. The first graph is a velocity graph of a basketball with respect to time, and it is assumed that it has been launched at an angle of 45 degrees and an initial velocity of 10 m/s. Due to air resistance, which I was able to include using Euler method, spreadsheet, and LoggerPro, the velocity asymptotically approaches -20m/s, which actually is the terminal velocity of a falling basketball.

However, I don't know what kind of equation is behind that graph.

The second graph is the deceleration from the air resistance, and I don't know what the equation for that one is either.

Homework Equations

Fd = 0.5 * Cd * rho * A * v^2

The Attempt at a Solution

I can't even guess what those graphs consist of...

 

[kuruman]

Please be precise with the terms that you are using. Here are some things to think about. You say

The first graph is a velocity graph of a basketball with respect to time, ...

I assume you mean the "vertical component of the velocity with respect to time ..."

The second graph is the deceleration from the air resistance, ...

What exactly do you mean by this? I think you really mean "acceleration". How do you interpret the plateau in the graph that shows the acceleration to be roughly constant between about 0.5 s and 1.0 s?

However, I don't know what kind of equation is behind that graph.

You quoted an equation under "relevant equations". Can you solve it? After solving it, is there a way you can you determine whether it is relevant or not? In other words can it explain your data?

 

[Dowon Kim]

Please be precise with the terms that you are using. Here are some things to think about. You say

"I assume you mean the "vertical component of the velocity with respect to time ...""

-Yeah, I do mean that. My bad.

"What exactly do you mean by this? I think you really mean "acceleration". How do you interpret the plateau in the graph that shows the acceleration to be roughly constant between about 0.5 s and 1.0 s?"

-Yes, it is acceleration, and I know that that constant region is due to the decreasing drag force when the basketball reaches the top of its projectile and therefore its velocity decreases.

"You quoted an equation under "relevant equations". Can you solve it? After solving it, is there a way you can you determine whether it is relevant or not? In other words can it explain your data?"

-It's the equation that I used to plot those graphs. Fd is the drag force, and all the variables other than v^2 are 0.0243, and v varies with time as two forces are acting on the basketball: gravity and air resistance.