What are the frequency and maximum velocity of a wheel rolling without slipping?

[stinlin]

Homework Statement

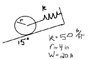
W = 20 lb
k = 50 lb/ft
r = 4 in.
Initially displaced 0.5 in.

Determine the frequency and maximum velocity of the wheel (which rolls without slipping).

Homework Equations

(theta) double dot + (w^2)theta = 0
(x) double dot + (w^2) (x) = 0

t = 2*pi / w

The Attempt at a Solution

I wrote out the initial information. The amplitude is 0.5 in. I didn't know which equation to use (the one with theta or with x). But I used the one with x and wrote out the moment balance and force balance, only to find that I was off.

I thought to use the theta equation, but I cannot figure out where to go with it. I know alpha = theta double dot. x = r(theta), but I don't know where to go from that either.

Any help and direction would be awesome! I have 2 other problems, but just understanding this one might get me going on the others.

 

[Mindscrape]

What level of physics is this? So the x equation will give you the spring's position as a function of time. Coincidentally, the angular velocity the spring moves with must also be the angular velocity of the wheel because the end of the spring is the center of wheel, and the center of the wheel determines the angular velocity.

The frequency can be determined from the angular velocity, and velocity from position and initial conditions (are you to assume the initial velocity is 0?).

Also, I think you are given a weight, which you will have to convert to slugs for the mass.

 

[stinlin]

This is an engineering Dynamics course. And yes, I'm assuming it to start from rest.