What are the torque-producing forces in this system?

[klandestine]

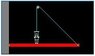
I've attached a picture of the problem I am referring to.

The pulley is placed so that the string makes a 45.0-degree angle with the beam. The beam is uniform, 5.00 meters long, and has weight w_{b}. The professor stands 2.00 meters from the pivot point and has weight w_{p}.

First, I am asked to find the tension in the string (in terms of w_{b} and w_{p}).

I started off by drawing a free body diagram. At the center of mass (which I found to be (\frac{5}{2}w_{b}+2w_{p})/(w_{b}+w_{p}), I have a force downward equal to w_{b}+w_{p}.
I also labeled both sections of the string as T (the first T vector is pointing straight up, and the second is pointing northwest)
I am unsure about these, but I suppose there is a normal force coming from the wall (horizontal) as well as a force of static friction pointing up.

Also, I am assuming that the pivot point is the point where the beam touches the wall.

So far, do I have the right idea?

 

[learningphysics]

Don't worry about center of mass. Draw a free body diagram of the beam. Presume that there is a vertical and horizontal force at the pivot point (there is a vertical force, but horizontal will turn out to be zero). Just better to have both if you're unsure.

Be careful about the forces acting on the beam. Where the professor is standing, I'd just put a force Fm (force of man on beam).

So the forces acting on the beam should be, the two forces at the pivot point, the weight of the beam, the force Fm, and the force T (tension) at the end of the beam.

Do you see a way to get a relationship between Fm and T (with no other unknowns in the equation)? One equation will do it.

Now you need a second equation relating Fm and T. Can you see how to get it? You may have to use a second free body diagram.

You have 2 equations with 2 unknowns, and you can solve for T.

 

[learningphysics]

You can draw the free body diagram of the professor-beam system. (treat the professor and beam as one body). I believe this is what you were doing. This is better than what I posted above. I don't know why I wanted to treat the professor and beam separately.

You don't need the center of mass. (you can calculate it if you wish to).

Make sure you draw all the forces acting on the beam and the professor.

One equation will let you immediately solve for T using this method.

 

[klandestine]

Would this equation be the net torque of the system (which equals zero)?

 

[klandestine]

here are my forces:
where the beam meets the wall - friction (up) normal (right)
on the beam I have Wp and Wb pointing down and the normal force of the professor pointing up
on the far right, I have the tension which has a both an up (T_y) and a left (T_x) pointing component.

But I feel odd about the forces that I attribute to the professor because I feel like him being attached to the pulley should lessen his weight and normal force.

 

[Doc Al]

here are my forces:
where the beam meets the wall - friction (up) normal (right)

It looks to me that the beam is attached to the wall. So the force that the wall exerts is not friction. But, no matter; if you are wise you will use the beam/wall interface as your pivot, so that force will exert no torque.

on the beam I have Wp and Wb pointing down and the normal force of the professor pointing up
on the far right, I have the tension which has a both an up (T_y) and a left (T_x) pointing component.

I would treat the professor plus beam as a single system. Using the left end of the beam as the pivot, the torque-producing forces are:

weight of the professor
weight of the beam
tension (T) pulling up on the professor
tension (T) pulling on the end of the beam (at an angle)​

Now just write the equation for rotational equilibrium.

(I'm saying just what learningphysics said in his last post.)