You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
What Causes Superimposition in String Fundamentals and Standing Waves?
- Thread starter lektor
- Start date
-
- Tags
- Fundamentals String
AI Thread Summary
In the fundamental mode of a vibrating string, the two impulses superimpose to create a standing wave, with the fixed ends determining the wavelength. The fundamental frequency corresponds to the longest wavelength, where the distance between the fixed ends equals the distance between two adjacent nodes, which is half a wavelength. Standing waves also occur in electrical signals, where they propagate through a channel and reflect back, achieving maximum transmission when the forward-to-reflected signal ratio is 1:1. The discussion raises questions about the physical boundaries of acoustic waves and their reflection. Understanding these principles is key to grasping wave behavior in both mechanical and electrical systems.
Physics news on Phys.org
Andrew Mason
Science Advisor
Homework Helper
- 7,794
- 502
The position of the fixed ends of the string determines the wavelength. The fundamental is the longest wavelength of vibration for which the distance between fixed ends is the distance between two adjacent nodes. Any longer wavelength would require the fixed end of the string to move. The distance between two adjacent nodes is 1/2 a wavelength.lektor said:This is not homework question but more of a personal interest question.
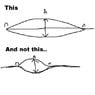
Can anyone help explain why it is that in the fundamental of a string the 2 impulses superimpose to form:
AM
Ouabache
Science Advisor
Homework Helper
- 1,345
- 8
With a string, what is the standing wave, standing between? 
With electrical signals, standing waves occur within a channel (wire, optical fiber etc.). The signal actually propagates the length of the channel and then radiates back. Maximum signal is transmitted when the forward/reflected ratio is 1:1
Thinking about the standing wave graph (time vs amplitude) that lektor gave, does the acoustic wave propagate out to a boundary and reflect back again to its origin? Where would be the physical position of the origin and boundary?
With electrical signals, standing waves occur within a channel (wire, optical fiber etc.). The signal actually propagates the length of the channel and then radiates back. Maximum signal is transmitted when the forward/reflected ratio is 1:1
Thinking about the standing wave graph (time vs amplitude) that lektor gave, does the acoustic wave propagate out to a boundary and reflect back again to its origin? Where would be the physical position of the origin and boundary?
TL;DR Summary: I came across this question from a Sri Lankan A-level textbook.
Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water.
I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system
$$M(t) = M_{C} + m(t)$$
$$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$
$$P_i = Mv + u \, dm$$
$$P_f = (M + dm)(v + dv)$$
$$\Delta P = M \, dv + (v - u) \, dm$$
$$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$
$$F = u \frac{dm}{dt} = \rho A u^2$$
from conservation of momentum , the cannon recoils with the same force which it applies.
$$\quad \frac{dm}{dt}...
Similar threads
- Replies
- 19
- Views
- 1K
- Replies
- 3
- Views
- 879
- Replies
- 29
- Views
- 1K
- Replies
- 9
- Views
- 2K
- Replies
- 3
- Views
- 4K
- Replies
- 1
- Views
- 1K
- Replies
- 31
- Views
- 4K
- Replies
- 2
- Views
- 1K
- Replies
- 7
- Views
- 2K
Hot Threads
-
Torque biomechanics
- Started by Naucus
- Replies: 6
- Introductory Physics Homework Help
-
Work Done in slowly pulling a thread
- Started by Bling Fizikst
- Replies: 28
- Introductory Physics Homework Help
-
How do you calculate the pull of this piston?
- Started by vdance
- Replies: 27
- Introductory Physics Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math