What force acts on the material of the capacitor in the Graham-Lahoz experiment?

[Alex Barri]

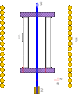
There is well known Graham–Lahoz experiment

G. M. Graham, D. G. Lahoz. Nature, 285, 154, 1980.

where "dispacement current" interreacts with constant magnetic field by Biot-Savart law.

It is OK! But a question appears - what namely force acts on the material of the capacitor??

I was very surprised nobody knows the answer !

 

[Meir Achuz]

Turning on the magnetic field induces a surface current that is up on your picture for one plate and down for the other. This current lasts until it gives a positive charge at the top of one plate and a negative charge at the top of the other plate. The F=qE provides a torque.

 

[Alex Barri]

Turning on the magnetic field induces a surface current that is up on your picture for one plate and down for the other. This current lasts until it gives a positive charge at the top of one plate and a negative charge at the top of the other plate. The F=qE provides a torque.

It is not true. In Graham-Lahoz experiment magnetic field is constant!

 

[Alex Barri]

Turning on the magnetic field is not possible!

 

[Alex Barri]

I am very pardon! I was wrong in understanding this experiment. There is no unusual :D