What Force Keeps the Block Stationary on a Frictionless Wedge?

[southernguy13]

Homework Statement

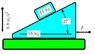
The surfaces between a 11 kg block, the 16 kg wedge and between the 16 kg wedge and the horizontal plane are smooth (without friction). The acceleration of gravity is 9.8 m/s2 .
A block is released on the inclined plane (top side of the wedge). What is the force F which must be exerted on the 16 kg block in order that the 11 kg block does not move up or down the plane? Answer in units of N.

Homework Equations

F=ma

The Attempt at a Solution

I drew a free body diagram with the i axis horizontal and the j axis vertical for each object, the block and the ramp. The block has a force of gravity, in the negative j direction and a normal force in the positive j direction. The acceleration of the block is 0.

I'm not sure how to figure out the exact free body for the ramp, since it's angled, or how to find what the force should be.

Thanks for the help!

 

[rl.bhat]

When you apply a force F on the larger block, it will accelerate a towards left. It will cause an a acceleration on the smaller block towards right. Resolve this acceleration into two components. One along the inclined plane in the upward direction and another perpendicular to the inclined pale. Similarly weight of the smaller block is resolved into two components. One along the inclined plane in the downward direction. and another perpendicular to the inclined plane. Now what should be the condition that the smaller block will remain at rest?