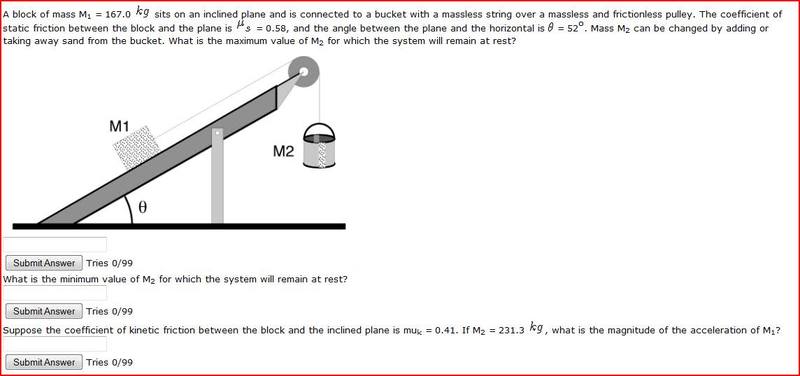
The discussion revolves around solving a block dynamics problem involving two masses, M1 and M2, and the forces affecting their motion. The user initially calculates the kinetic friction force and acceleration but struggles to arrive at the correct answer. Key points include the necessity of incorporating the vertical component of M1's weight and recognizing that the total mass of both M1 and M2 must be considered when calculating acceleration. The conversation highlights the importance of accurately summing forces and understanding the relationship between the two masses in motion. Ultimately, the user seeks clarification on their calculations and the correct approach to find the acceleration of M1.