hittce
- 5
- 0
Homework Statement
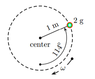
The questions asks for the centripetal acceleration of the mass in the vertical circle shown in the picture. It also states the object has exactly enough velocity to maintain a vertical circle.
Homework Equations
F=ma, a=v^2/r
The Attempt at a Solution
I've tried solving for the velocity by setting mg=m*v^2/r and then subtracting mgcos(114) to get the velocity and then plugging it back into a=v^2/r, but to no avail.