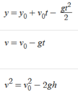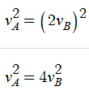What is the Correct Calculation for h/H When Ball A Collides with Ball B?

[Juliusz]

Homework Statement

Ball A is dropped from rest from a building of height H exactly as ball B is thrown up vertically from the ground. When they collide A has twice the speed of B. If the collision occurs at height h, what is h/H?

Homework Equations

(I would type them out put I can't format them properly, sorry)

The Attempt at a Solution

I did everything as in the example, but then I got to the part where we compare the speeds. The formula (red arrow) show that at the time of impact, the speed of A is 4 times greater than speed of B. But in the problem, it states that the speed of A is only twice the speed of B. So my understanding is that there should be a 2 instead of a 4. Am I missing something?

 

[PeroK]

Am I missing something?

The equation is in $v^2$.

 

[Juliusz]

Ah, I think I see. So it can be written like this?

 

[neilparker62]

Alternate method based on relative velocity of A and B as well as the speed relation when they collide:

Solve simultaneously for H and t (in terms of u - initial velocity of B - and g):

t = H/u ......Eqn 1
2(u-gt) = gt ....Eqn 2

Then h = ut - 0.5 g t^2.