What is the current in each resistor in a complex RC circuit?

[kevbot010]

Homework Statement

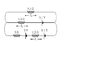
Find the current I1 in the 1.2
resistor
at the bottom of the circuit between the two
power supplies.
Answer in units of A.
015 (part 2 of 3) 10.0 points
Determine I2.
Answer in units of A.
016 (part 3 of 3) 10.0 points
Determine I3.
Answer in units of A.

Homework Equations

I=Ifinal(e^-t/RC)
V=IR

The Attempt at a Solution

V=IR
I=V/R
I=9.5/1.2
I=7.91667A

The attachment is a picture of the circuit. I really have no idea how to solve this and could use some helpful explanation. Thanks!

Kevin

 

[kevbot010]

ok i understand i must use the loop rule and the junction rule.

I made it where there are two loops
Loop1:
9.5-1.2I1+2-3-5.4I2-3.1=0

Loop2:
3.1-5.4I2-8.4I3=0

I think this may be right, if it is i am still unsure of how to continue with the problem