What Is the Difference Between Moment and Bending Moment in Beam Calculations?

[___]

Hello, I have a small question about moments and bending moments.

So, if I have a beam with a loading given by q (N/m) which is given as a function of x then what do these calculations get me?

\int xq(x) dx
\int (\int q(x) dx) dx

The first integral gives me the moment about a point because I am taking a differential distance and multiplying it with the value of Force there given by q(x) and adding up all these differential moments.

The second integral gives me the bending moment about a point..

And here is what has been troubling me.

Isn't the bending moment the resultant moment on one side of the beam? I mean:

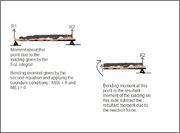
So, isn't the bending moment at a point simply the first equation where you integrate from the point you are interested into the end and then subtract the moment due to the reaction?

So, bending moment = (\int_{x}^L xq(x) dx ) - R2x

But that that doesn't seem right. Since the bending moment is \int (\int q(x) dx) dx
and you fill in the boundary conditions and plug in the value of where you want it...

In short, what is the fundamental difference between the bending moment and the resultnt moment on one side of the beam. To me it seems they are the same, the bending moment is the moment the beam is having to apply at that point to counteract the resultant moment on the other side of the beam, but mathematically they seem different.

 

[Studiot]

There are several difficulties with your approach.

Why are you not following convention and working from left to right?

If you do not do this you need a negative sign in you equations since the positive x increasing direction is left to right.

Secondly the integration only works like this with distributed loads, not with point loads.

 

[___]

There are several difficulties with your approach.

Why are you not following convention and working from left to right?

If you do not do this you need a negative sign in you equations since the positive x increasing direction is left to right.

Oh ok, fair enough.

Secondly the integration only works like this with distributed loads, not with point loads.

Yeah. I was looking at beams with point loads but it was too difficult to come up with an expression that described the bending moment (because it was described piecewise with discontinuity in shear forces) so I gave up.


I think I see the problem with my expressions though. Once I take a cut like I have done in the picture, I should still be able to use the force X distance method to work out the moment due to the load and the reaction. But however, since I took my cut this way I need to look at the fact that the loading is described by q as a function of x which begins from the reaction at the left hand side.

So, the expression for moment using the Force X distance becomes a little more complicated since the distance is the distance from the point where I have taken the cut, and the loading is being described through the variable x which is measuring the distance from the left reaction. So I need to find an expression that associates the distance x with the distance from the cut, which is going to be a little difficult.

Thanks for the reply.

 

[Studiot]

Whatever direction conventions you choose you will have to cope with the fact that for many loading conditions the relevant equations, expressed as functions of x, are different on different parts of the beam.

An elegant solution to this is Macaulay's method

A google search will reveal many hits eg

http://www.colincaprani.com/files/notes/SAIII/Macaulay's Method 1011.pdf

There are also some worked examples in recent threads in Physics Forums on this - try a search.

go well