What is the direction of work in this figure?

[patric44]

Homework Statement

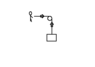
find the direction of work in this figure ?

Relevant Equations

w= F.d

iam not sure of the direction of work , is it positive becouse pulleys change the direction of the force ? or is it negative because of the arrow that indicates the direction of acceleration ??!

 

[Orodruin]

The work done by what force on what object? Your drawing does not look like a proper free-body diagram. A FBD should involve only one object and all of the external forces acting on this object.

 

[patric44]

the work done by the person to lift that mass , this diagram is an exact replica to the example

 

[Orodruin]

the work done by the person to lift that mass

There is no such thing. There is the "work done by the person on the mass". That work is positive because the force by the person on the mass (or rather, the rope) is in the same direction as the displacement when the mass is lifted. Then there is the "work done by the mass on the person", which would be the opposite because it is the same displacement but the force is the Newton 3 pair of the force of the person on the mass, i.e., it is equal in magnitude and opposite in direction.

 

[patric44]

There is no such thing. There is the "work done by the person on the mass". That work is positive because the force by the person on the mass (or rather, the rope) is in the same direction as the displacement when the mass is lifted. Then there is the "work done by the mass on the person", which would be the opposite because it is the same displacement but the force is the Newton 3 pair of the force of the person on the mass, i.e., it is equal in magnitude and opposite in direction.

so the person work on the mass is + , but i have a question here what is the arrow in front of the person indicates , its some how strange that its opposite to the tension force ? as if its indicating the acceleration of the system indicating a negative work or something ?!

 

[Orodruin]

so the person work on the mass is + , but i have a question here what is the arrow in front of the person indicates , its some how strange that its opposite to the tension force ? as if its indicating the acceleration of the system indicating a negative work or something ?!

Tension in itself is not a force, it is technically a tensor that gives you a force depending on which object you are drawing the FBD for. If you are drawing the FBD for the person, then the force resulting from the tension is directed to the right (it is the tension in the rope multiplied by the direction of the rope away from the object you are drawing the FBD for). You should forget you ever saw that figure, it is a very bad figure that just seems designed to confuse.