L_landau
- 27
- 0
Homework Statement
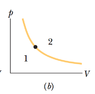
The dot in Fig. 19-18b represents the initial state of a gas, and the isotherm through the dot divides the p-V diagram into regions 1 and 2. For the following processes, determine whether the change Eint in the internal energy of the gas is positive, negative, or zero: (a) the gas moves up along the isotherm, (b) it moves down along the isotherm, (c) it moves to anywhere in region 1, and (d) it moves to anywhere in region 2.
Homework Equations
ΔEint = Q - W (by the system)
or
ΔEint = Q + W (on the system)
The Attempt at a Solution
(a)/(b) As the gas moves along the isotherm there is no change in temperature and thus no ΔEint. My problem comes in (c) when the gas moves to the right. This would mean that positive work is done by the system, which would mean that ΔEint = Q - W. Why is it that ΔEint is actually positive in this case?