What is the final angular velocity of each cylinder

[samm12345]

Homework Statement

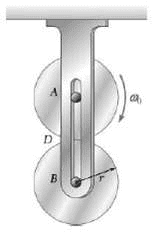
The uniform 4-kg cylinder A, of radius r = 150 mm, has an angular velocity w = 50 rad/s when it is brought into contact with an identical cylinder B which is at rest. The coefficient of kinetic friction at the contact point D is uk. After a period of slipping, the cylinders attain constant angular velocities of equal magnitude and opposite direction at the same time. Knowing that cylinder A executes three revolutions before it attains a constant angular velocity and cylinder B executes one revolution before it attains a constant angular velocity, determine
(a) The final angular velocity of each cylinder,
(b) The coefficient of kinetic friction uk.

Relevant Equations

T1 + U =T2

Problem Statement: The uniform 4-kg cylinder A, of radius r = 150 mm, has an angular velocity w = 50 rad/s when it is brought into contact with an identical cylinder B which is at rest. The coefficient of kinetic friction at the contact point D is uk. After a period of slipping, the cylinders attain constant angular velocities of equal magnitude and opposite direction at the same time. Knowing that cylinder A executes three revolutions before it attains a constant angular velocity and cylinder B executes one revolution before it attains a constant angular velocity, determine
(a) The final angular velocity of each cylinder,
(b) The coefficient of kinetic friction uk.
Relevant Equations: T1 + U =T2

 

[berkeman]

Welcome to the PF.

We require that you show your work toward the solution before we can offer tutorial help. Please show us how you are approaching the problem...