madah12
- 326
- 1
Homework Statement
show that
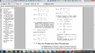
xf(x)=integral from 0 to infinity of [B*(w)sin(wx)]dw , // B* is a function not B * w
where B* = -dA/dw
A(w) = 2/pi integral from 0 to infinity [f(v) cos(wv)] dv
Homework Equations
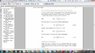
f(x)=integral from 0 to infinity [A(w)cos(wx)] dwThe Attempt at a Solution
working on right hand side
B*= 2/pi * integral from 0 to infinity [vf(v)cos(wv)dv]
=integral from 0 to infinity of [2/pi * integral from 0 to infinity [vf(v)cos(wv)dv]sin(wx)]dw
left side = integral from 0 to infinity [ A(w)xcos(wx)]dw
Even when i tried writing A as integral i don't see how do i prove 2 sides which have 2 integrals in them equal each other?